
【題目】在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點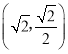 .
.
(1)求橢圓![]() 的方程;
的方程;
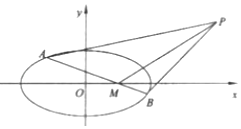
(2)設點![]() ,點
,點![]() 在
在![]() 軸上,過點
軸上,過點![]() 的直線交橢圓
的直線交橢圓![]() 交于
交于![]() ,
,![]() 兩點.
兩點.
①若直線![]() 的斜率為
的斜率為![]() ,且
,且![]() ,求點
,求點![]() 的坐標;
的坐標;
②設直線![]() ,
,![]() ,
,![]() 的斜率分別為
的斜率分別為![]() ,
,![]() ,
,![]() ,是否存在定點
,是否存在定點![]() ,使得
,使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 點坐標;若不存在,請說明理由.
點坐標;若不存在,請說明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②存在,
;②存在,![]() .
.
【解析】
(1)利用橢圓的離心率為![]() 、過點
、過點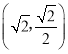 以及
以及![]() 建立方程組,求出
建立方程組,求出![]() 和
和![]() 的值即可;
的值即可;
(2)①設出直線![]() 的方程,聯立直線與橢圓的方程,結合韋達定理和
的方程,聯立直線與橢圓的方程,結合韋達定理和![]() ,得出
,得出![]() 的值即可;②假設
的值即可;②假設![]() 成立,設
成立,設![]() ,分別討論直線
,分別討論直線![]() 的斜率是否為
的斜率是否為![]() 的情形,聯立直線與圓錐曲線的方程以及利用
的情形,聯立直線與圓錐曲線的方程以及利用![]() ,解出
,解出![]() 的值,求出
的值,求出![]() 點坐標即可.
點坐標即可.
(1)![]() 橢圓
橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() .
.
![]()
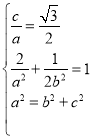 ,解之得:
,解之得: ,
,
![]() 橢圓
橢圓![]() 的方程為:
的方程為:![]() ;
;
(2)設![]() ,
,![]() ,
,
①設直線![]() 的方程為:
的方程為:![]() ,
,
由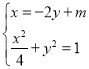 ,得:
,得:![]() ,
,
![]() ,故
,故![]() ,
,
![]()
![]() ,
,![]() ,
,
![]()
![]() ,解得
,解得![]() .
.
![]()
![]() ;
;
②![]() ,設
,設![]() ,
,
(ⅰ)當直線![]() 的斜率為
的斜率為![]() 時,
時,![]() ,
,![]() ,
,
由![]() ,可得
,可得![]() ,解得
,解得![]() ,即
,即![]() ;
;
(ⅱ)當直線![]() 的斜率不為
的斜率不為![]() 時,設
時,設![]() ,
,![]() ,
,
設直線![]() 的方程為
的方程為![]() ,
,
由 ,得:
,得:![]()
![]()
![]() ,
,![]() .
.
由![]() ,可得
,可得![]() ,
,
 ,
,
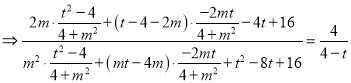 ,
,
![]() ,
,
![]() ,
,
![]() 當
當![]() 時,上式恒成立.
時,上式恒成立.
綜上,存在定點![]() ,使得
,使得![]() 恒成立.
恒成立.


科目:高中數學 來源: 題型:
【題目】有關命題的說法錯誤的是( )
A.若p∨q為假命題,則p、q均為假命題
B.“x=1”是“x2﹣3x+2=0”的充分不必要條件
C.命題“若x2﹣3x+2=0,則x=1”的逆否命題為:“若x≠1,則x2﹣3x+2≠0”
D.對于命題p:x≥0,2x=3,則¬P:x<0,2x≠3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在多面體![]() 中,平面
中,平面![]() 平面
平面![]() .四邊形
.四邊形![]() 為正方形,四邊形
為正方形,四邊形![]() 為梯形,且
為梯形,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
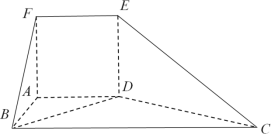
(1)求證:![]() ;
;
(2)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(3)線段![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 平面
平面![]() 若存在,求
若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() ,長半軸長與短半軸長的差為
,長半軸長與短半軸長的差為![]() ,離心率為
,離心率為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若在![]() 軸上存在點
軸上存在點![]() ,過點
,過點![]() 的直線
的直線![]() 分別與橢圓
分別與橢圓![]() 相交于
相交于![]() 、
、![]() 兩點,且
兩點,且![]() 為定值,求點
為定值,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現要完成下列3項抽樣調查:①從20罐奶粉中抽取4罐進行食品安全衛生檢查;②從某社區100戶高收入家庭,270戶中等收入家庭,80戶低收入家庭中選出45戶進行消費水平調查;③某中學報告廳有28排,每排有35個座位,一次報告會恰好坐滿了聽眾,報告會結束后,為了聽取意見,需要請28名聽眾進行座談.較為合理的抽樣方法是( )
A.①系統抽樣;②簡單隨機抽樣;③分層抽樣
B.①簡單隨機抽樣;②分層抽樣;③系統抽樣
C.①分層抽樣;②系統抽樣;③簡單隨機抽樣
D.①簡單隨機抽樣;②系統抽樣;③分層抽樣
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線x2=4y.

(1)求拋物線在點P(2,1)處的切線方程;
(2)若不過原點的直線l與拋物線交于A,B兩點(如圖所示),且OA⊥OB,|OA|=![]() |OB|,求直線l的斜率.
|OB|,求直線l的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知點![]() 在圓柱
在圓柱![]() 的底面圓
的底面圓![]() 上,
上,![]() 為圓
為圓![]() 的直徑.
的直徑.
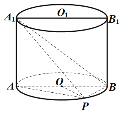
(1)若圓柱![]() 的體積
的體積![]() 為
為![]() ,
,![]() ,
,![]() ,求異面直線
,求異面直線![]() 與
與![]() 所成的角(用反三角函數值表示結果);
所成的角(用反三角函數值表示結果);
(2)若圓柱![]() 的軸截面是邊長為2的正方形,四面體
的軸截面是邊長為2的正方形,四面體![]() 的外接球為球
的外接球為球![]() ,求
,求![]() 兩點在球
兩點在球![]() 上的球面距離.
上的球面距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年的政府工作報告強調,要樹立綠水青山就是金山銀山理念,以前所未有的決心和力度加強生態環境保護.某地科技園積極檢查督導園區內企業的環保落實情況,并計劃采取激勵措施引導企業主動落實環保措施,下圖給出的是甲、乙兩企業2012年至2017年在環保方面投入金額(單位:萬元)的柱狀圖.
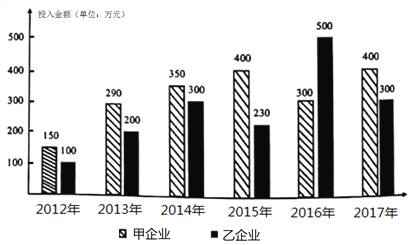
(Ⅰ)分別求出甲、乙兩企業這六年在環保方面投入金額的平均數;(結果保留整數)
(Ⅱ)園區管委會為盡快落實環保措施,計劃對企業進行一定的獎勵,提出了如下方案:若企業一年的環保投入金額不超過200萬元,則該年不獎勵;若企業一年的環保投入金額超過200萬元,不超過300萬元,則該年獎勵20萬元;若企業一年的環保投入金額超過300萬元,則該年獎勵50萬元.
(ⅰ)分別求出甲、乙兩企業這六年獲得的獎勵之和;
(ⅱ)現從甲企業這六年中任取兩年對其環保情況作進一步調查,求這兩年獲得的獎勵之和不低于70萬元的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com