
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,短軸長為4.
,短軸長為4.
(1)求橢圓C的標準方程.
(2)設直線l過點(2,0)且與橢圓C相交于不同的兩點A、B,直線![]() 與x軸交于點D,E是直線
與x軸交于點D,E是直線![]() 上異于D的任意一點,當
上異于D的任意一點,當![]() 時,直線BE是否恒過x軸上的定點?若過,求出定點坐標,若不過,請說明理由。
時,直線BE是否恒過x軸上的定點?若過,求出定點坐標,若不過,請說明理由。
【答案】(1)![]() (2)直線BE恒過x軸上的定點
(2)直線BE恒過x軸上的定點![]() ,詳見解析
,詳見解析
【解析】
(1)利用離心率![]() ,短軸長4,列關于
,短軸長4,列關于![]() 的方程組,解方程即可求得橢圓C的標準方程。
的方程組,解方程即可求得橢圓C的標準方程。
(2)當斜率不存在時,可得直線BE過定點![]() ,當斜率存在時,
,當斜率存在時,![]() ,設出
,設出![]() 的坐標,求出直線BE的方程,求出與x軸的交點表達式
的坐標,求出直線BE的方程,求出與x軸的交點表達式![]() ,即證
,即證![]() ,
,
根據![]() 的特點,將直線l和橢圓聯立,得到
的特點,將直線l和橢圓聯立,得到![]() ,代入
,代入![]() ,可得式子成立,即證明直線BE恒過x軸上的定點
,可得式子成立,即證明直線BE恒過x軸上的定點![]() 。
。
解:(1)由題意得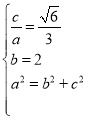 。解得
。解得![]() ,
,
所以橢圓C的標準方程為![]()
(2)直線BE恒過x軸上的定點![]()
證明如下:
因為![]() .所以
.所以![]() ,
,
因為直線l過點![]()
①當直線l的斜率不存在時,則直線l的方程為![]() ,
,
不妨設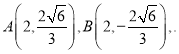 則
則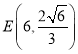
此時,直線BE的方程為![]() ,
,
所以直線BE過定點![]() ;
;
②直線l的斜率存在且不為零時,設直線l的方程為![]() ,
,![]() ,所以
,所以![]() .
.
直線![]() ,令
,令![]() ,得
,得![]()
即![]() ,又
,又![]()
所以![]()
即證![]()
即證![]()
聯立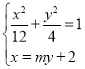 ,消x得
,消x得![]() ,
,
因為點![]() 在C內,所以直線l與C恒有兩個交點,
在C內,所以直線l與C恒有兩個交點,
由韋達定理得,![]()
代入(*)中得![]()
所以直線BE過定點![]() ,
,
綜上所述,直線BE恒過x軸上的定點![]() .
.


科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是正方形,且
是正方形,且![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,![]() ,點
,點![]() 為線段
為線段![]() 的中點,點
的中點,點![]() 是線段
是線段![]() 上的一個動點.
上的一個動點.
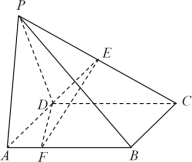
(Ⅰ)求證:平面![]()
![]() 平面
平面![]() ;
;
(Ⅱ)設二面角![]() 的平面角為
的平面角為![]() ,試判斷在線段
,試判斷在線段![]() 上是否存在這樣的點
上是否存在這樣的點![]() ,使得
,使得![]() ,若存在,求出
,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某冰糖橙,甜橙的一種,云南著名特產,以味甜皮薄著稱。該橙按照等級可分為四類:珍品、特級、優級和一級(每箱5kg).某采購商打算采購一批橙子銷往省外,并從采購的這批橙子中隨機抽取100箱,利用橙子的等級分類標準得到的數據如下表:
等級 | 珍品 | 特級 | 優級 | 一級 |
箱數 | 40 | 30 | 10 | 20 |
售價(元/kg) | 36 | 30 | 24 | 18 |
(1)試計算樣本中的100箱不同等級橙子的平均價格;
(2)按照分層抽樣的方法,從這100個樣本中抽取10箱,試計算各等級抽到的箱數;
(3)若在(2)抽取的特級品和一級品的箱子上均編上號放在一起再從中抽取2箱,求抽取的2箱中兩種等級均有的概率
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,曲線![]() :
:![]() ,(
,(![]() 為參數),將曲線
為參數),將曲線![]() 上的所有點的橫坐標縮短為原來的
上的所有點的橫坐標縮短為原來的![]() ,縱坐標縮短為原來的
,縱坐標縮短為原來的![]() 后得到曲線
后得到曲線![]() ,以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標方程為
,以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,直線l的極坐標方程為 。
。
(1)求曲線![]() 的極坐標方程和直線l的直角坐標方程;
的極坐標方程和直線l的直角坐標方程;
(2)設直線l與曲線![]() 交于不同的兩點A,B,點M為拋物線
交于不同的兩點A,B,點M為拋物線![]() 的焦點,求
的焦點,求![]() 的值。
的值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“大眾創業,萬眾創新”是李克強總理在本屆政府工作報告中向全國人民發出的口號.某生產企業積極響應號召,大力研發新產品,為了對新研發的一批產品進行合理定價,將該產品按事先擬定的價格進行試銷,得到一組銷售數據![]() (
(![]() =1,2,…,6),如表所示:
=1,2,…,6),如表所示:
試銷單價 | 4 | 5 | 6 | 7 | 8 | 9 |
產品銷量 | q | 84 | 83 | 80 | 75 | 68 |
已知![]() .
.
(Ⅰ)求出![]() 的值;
的值;
(Ⅱ)已知變量![]() 具有線性相關關系,求產品銷量
具有線性相關關系,求產品銷量![]() (件)關于試銷單價
(件)關于試銷單價![]() (元)的線性回歸方程
(元)的線性回歸方程![]() ;
;
(參考公式:線性回歸方程中![]() ,
,![]() 的最小二乘估計分別為
的最小二乘估計分別為 ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A. 設![]() 是實數,若方程
是實數,若方程![]() 表示雙曲線,則
表示雙曲線,則![]() .
.
B. “![]() 為真命題”是“
為真命題”是“![]() 為真命題”的充分不必要條件.
為真命題”的充分不必要條件.
C. 命題“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ,
,![]() ”.
”.
D. 命題“若![]() 為
為![]() 的極值點,則
的極值點,則![]() ”的逆命題是真命題.
”的逆命題是真命題.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC的內角A,B,C所對應的邊分別為a,b,c.
(Ⅰ)若a,b,c成等差數列,證明:sinA+sinC=2sin(A+C);
(Ⅱ)若a,b,c成等比數列,求cosB的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓C:![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,其左焦點到點P(2,1)的距離為
,其左焦點到點P(2,1)的距離為![]() .不過原點O的直線l與C相交于A,B兩點,且線段AB被直線OP平分.
.不過原點O的直線l與C相交于A,B兩點,且線段AB被直線OP平分.
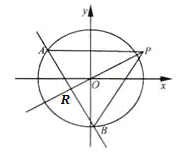
(Ⅰ)求橢圓C的方程;
(Ⅱ) 求![]() ABP的面積取最大時直線l的方程.
ABP的面積取最大時直線l的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com