
(本題滿分14分)如圖,有一塊邊長為1(百米)的正方形區域ABCD,在點A處有一個可轉動的探照燈,其照射角 始終為
始終為 (其中點P,Q分別在邊BC,CD上),設
(其中點P,Q分別在邊BC,CD上),設 .
.

(Ⅰ)用t表示出PQ的長度,并探求 的周長l是否為定值;
的周長l是否為定值;
(Ⅱ)問探照燈照射在正方形ABCD內部區域陰影部分的面積S最大為多少(平方百米)?
(1) =定值;
=定值;
(2)探照燈照射在正方形 內陰影部分的面積
內陰影部分的面積 最大為
最大為 平方百米.
平方百米.
解析試題分析:(1) 結合三角函數定義得到DQ的值。和勾股定理得到PQ的值,求解周長。
結合三角函數定義得到DQ的值。和勾股定理得到PQ的值,求解周長。
(2)根據間接法得到所求解的面積表達式,運用不等式的思想求解得到最值。
 ---2分
---2分 -------------------------------------------------4分
-------------------------------------------------4分 ---------------------6分
---------------------6分 =定值--------------------------------7分
=定值--------------------------------7分 -----------------------10分
-----------------------10分 --------------------------------------------------12分
--------------------------------------------------12分 -----------------------------------------13分
-----------------------------------------13分
所以探照燈照射在正方形 內陰影部分的面積
內陰影部分的面積 最大為
最大為 平方百米.----14分
平方百米.----14分
考點:本試題主要考查了利用三角函數的性質和三角函數的定義得到邊長和面積的表示的運用。
點評:解決該試題的關鍵是能合理的設出變量表述各個邊長,并能得到其面積的表示,結合均值不等式得到最值。


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案科目:高中數學 來源: 題型:解答題
(本小題共12分)
已知函數f(t)= 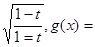
 ]
]
(Ⅰ)將函數g(x)化簡成Asin(ωx+φ)+B(A>0,ω>0,φ∈[0,2π))的形式;
(Ⅱ)求函數g(x)的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分13分)已知函數
(I)求函數f(x)的最小正周期和單調增區間;
(Ⅱ)函數f(x)的圖象可以由函數y=sin2x(x∈R)的圖象經過怎樣的變換得到?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com