
(本小題滿分12分)
在 中,角
中,角 所對的三邊分別為
所對的三邊分別為 成等比數列,且
成等比數列,且 .
.
(1)求 的值;
的值;
(2)設 ,求
,求 的值.
的值.
(1)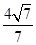 ;(2)3.
;(2)3.
解析試題分析:(1)由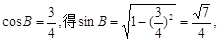 …………2分
…………2分
因為 成等比數列,所以
成等比數列,所以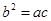 .則
.則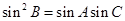 .則
.則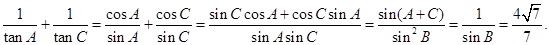
或者由 ,得到
,得到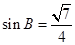 .…………6分
.…………6分
(2)因為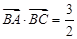 ,由向量數量積公式,得
,由向量數量積公式,得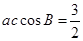 .
.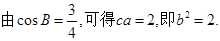 …………8分
…………8分
由余弦定理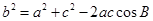 ,所以
,所以 .則
.則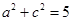 ……10分
……10分
所以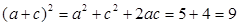 .因此
.因此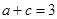 .…………12分
.…………12分
考點:等比數列的性質;同角三角函數關系式;和差公式;正弦定理;余弦定理;向量數量積公式。
點評:三角函數和其他知識點相結合往往是一道大題,一般較為簡單,應該是必得分的題目。而有些同學在學習中認為這類題簡單,自己一定會,從而忽略了對它的練習,因此導致考試時不能得滿分,甚至不能得分。比如此題在第二問中,就較易忘掉應用第一問求出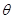 的范圍。因此我們在平常訓練的時候就要要求自己“會而對,對而全”。
的范圍。因此我們在平常訓練的時候就要要求自己“會而對,對而全”。


 特高級教師點撥系列答案
特高級教師點撥系列答案科目:高中數學 來源: 題型:解答題
(本小題滿分10分)
函數f(x)=Asin(ωx-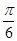 )+1(A>0,ω>0)的最大值為3,其圖象相鄰兩條對稱軸之間的距離為
)+1(A>0,ω>0)的最大值為3,其圖象相鄰兩條對稱軸之間的距離為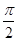 .
.
(1)求函數f(x)的解析式;
(2)設α∈(0,2π),f(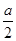 )=2,求α的值.
)=2,求α的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)已知函數 (
( ),直線
),直線 ,
, 是
是 圖象的任意兩條對稱軸,且
圖象的任意兩條對稱軸,且 的最小值為
的最小值為 .
.
(I)求 的表達式;
的表達式;
(Ⅱ)將函數 的圖象向右平移
的圖象向右平移 個單位后,再將得到的圖象上各點的橫坐標伸長為原來的2倍,縱坐標不變,得到函數
個單位后,再將得到的圖象上各點的橫坐標伸長為原來的2倍,縱坐標不變,得到函數 的圖象,若關于
的圖象,若關于 的方程
的方程 ,在區間
,在區間 上有且只有一個實數解,求實數
上有且只有一個實數解,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分14分)如圖,有一塊邊長為1(百米)的正方形區域ABCD,在點A處有一個可轉動的探照燈,其照射角 始終為
始終為 (其中點P,Q分別在邊BC,CD上),設
(其中點P,Q分別在邊BC,CD上),設 .
.

(Ⅰ)用t表示出PQ的長度,并探求 的周長l是否為定值;
的周長l是否為定值;
(Ⅱ)問探照燈照射在正方形ABCD內部區域陰影部分的面積S最大為多少(平方百米)?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com