
己知a,b,c,d∈(0,+∞),且a>b.設P=![]() ,Q=
,Q=![]() ,M=
,M=![]() ,N=
,N=![]() ,那么P,Q,M,N的大小順序為
,那么P,Q,M,N的大小順序為
[ ]
|
解法一: (使用不等式性質定理推證)∵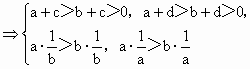 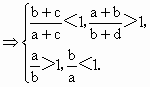
∴ P<1,N<1,Q>1,M>1.又∵ M=由 b+d>b>0得
∵ a>b,∴a-b>0,∴∴ 1+同理可證: N>P.∴ P<N<M<Q此法展示了不等式性質定理的應用,同時培養了學生使用不等式的性質定理進行推理論證的能力. 解法二: (利用函數的單調性比較兩數大小)由 P=1-∵ a>b,∴a-b>0.從而知函數 f(x)=1-又 a,c∈(0,+∞),∴a+c>Q.∴ P=f(a)<f(a+c)=N<1.同理: Q=1+∴ P<N<M<Q答案選 C. |
|
利用函數的單調性比較兩數大小的解題思路是:①整理變形兩數 (式);②聯想所學的初等函數,使所討論的兩數(式)為該函數的兩個函數值;③由函數的單調性,確定兩數(式)的大小.通過構造函數比較大小,可以培養學生分析問題的能力,滲透變與不變的辯證思想與轉化思想. |


 口算小狀元口算速算天天練系列答案
口算小狀元口算速算天天練系列答案科目:高中數學 來源: 題型:
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分不必要條件 |
| B、必要不充分條件 |
| C、既不充分也不必要條件 |
| D、充要條件 |
查看答案和解析>>
科目:高中數學 來源: 題型:
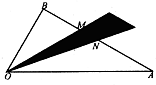 如圖,己知|
如圖,己知|| OA |
| OB |
| OP |
| OA |
| OB |
| A、①②④ | B、①③④ |
| C、①③⑤ | D、②⑤ |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題

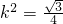
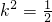
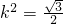
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com