
【題目】《九章算術》中,將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬,將四個面都為直角三角形的四面體稱之為鱉臑.如圖,在陽馬P﹣ABCD中,側棱PD⊥底面ABCD,且PD=CD,過棱PC的中點E,作EF⊥PB交PB于點F,連接DE,DF,BD,BE. 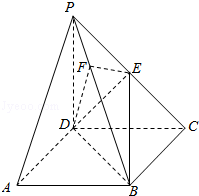
(1)證明:PB⊥平面DEF.試判斷四面體DBEF是否為鱉臑,若是,寫出其每個面的直角(只需寫出結論);若不是,說明理由;
(2)若面DEF與面ABCD所成二面角的大小為 ![]() ,求
,求 ![]() 的值.
的值.
【答案】
(1)證明:解法1:因為PD⊥底面ABCD,所以PD⊥BC,
由底面ABCD為長方形,有BC⊥CD,而PD∩CD=D,
所以BC⊥平面PCD.而DE平面PDC,所以BC⊥DE.
又因為PD=CD,點E是PC的中點,所以DE⊥PC.
而PC∩CB=C,所以DE⊥平面PBC.而PB平面PBC,所以PB⊥DE.
又PB⊥EF,DE∩FE=E,所以PB⊥平面DEF.
由DE⊥平面PBC,PB⊥平面DEF,可知四面體BDEF的四個面都是直角三角形,
即四面體BDEF是一個鱉臑,其四個面的直角分別為∠DEB,∠DEF,∠EFB,∠DFB
解法2:
以D為原點,射線DA,DC,DP分別為x,y,z軸的正半軸,建立空間直角坐標系.設PD=DC=1,BC=λ,
則D(0,0,0),P(0,0,1),B(λ,1,0),C(0,1,0), ![]() =(λ1,﹣1),點E是PC的中點,所以E(0,
=(λ1,﹣1),點E是PC的中點,所以E(0, ![]() ,
, ![]() ),
), ![]() =(0,
=(0, ![]() ,
, ![]() ),
),
于是 ![]() =0,即PB⊥DE.
=0,即PB⊥DE.
又已知EF⊥PB,而ED∩EF=E,所以PB⊥平面DEF.
因 ![]() =(0,1,﹣1),
=(0,1,﹣1), ![]() =0,則DE⊥PC,所以DE⊥平面PBC.
=0,則DE⊥PC,所以DE⊥平面PBC.
由DE⊥平面PBC,PB⊥平面DEF,可知四面體BDEF的四個面都是直角三角形,
即四面體BDEF是一個鱉臑,其四個面的直角分別為∠DEB,∠DEF,∠EFB,∠DFB
(2)解法1:如圖1,
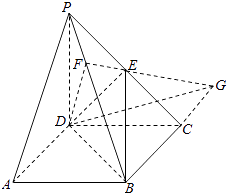
在面BPC內,延長BC與FE交于點G,則DG是平面DEF與平面ACBD的交線.
由(1)知,PB⊥平面DEF,所以PB⊥DG.
又因為PD⊥底面ABCD,所以PD⊥DG.而PD∩PB=P,所以DG⊥平面PBD.
所以DG⊥DF,DG⊥DB
故∠BDF是面DEF與面ABCD所成二面角的平面角,
設PD=DC=1,BC=λ,有BD= ![]() ,
,
在Rt△PDB中,由DF⊥PB,得∠DPB=∠FDB= ![]() ,
,
則 tan ![]() =tan∠DPF=
=tan∠DPF= ![]() =
= ![]() =
= ![]() ,解得
,解得 ![]() .
.
所以 ![]() =
= ![]() =
= ![]()
故當面DEF與面ABCD所成二面角的大小為 ![]() 時,
時, ![]() =
= ![]()
解法2:
由PD⊥底面ABCD,所以 ![]() =(0,0,1)是平面ACDB的一個法向量;
=(0,0,1)是平面ACDB的一個法向量;
由(1)知,PB⊥平面DEF,所以 ![]() =(﹣λ,﹣1,1)是平面DEF的一個法向量.
=(﹣λ,﹣1,1)是平面DEF的一個法向量.
若面DEF與面ABCD所成二面角的大小為 ![]() ,
,
則運用向量的數量積求解得出cos ![]() =
= ![]() =
= ![]() ,
,
解得 ![]() .所以所以
.所以所以 ![]() =
= ![]() =
= ![]()
故當面DEF與面ABCD所成二面角的大小為 ![]() 時,
時, ![]() =
= ![]()
【解析】(1)解法1:直線與直線,直線與平面的垂直的轉化證明得出PB⊥EF,DE∩FE=E,所以PB⊥平面DEF,即可判斷DE⊥平面PBC,PB⊥平面DEF,可知四面體BDEF的四個面都是直角三角形,確定直角. 解法2:以D為原點,射線DA,DC,DP分別為x,y,z軸的正半軸,建立空間直角坐標系,運用向量的數量積判斷即可.
(2.)根據公理2得出DG是平面DEF與平面ACBD的交線.利用直線平面的垂直判斷出DG⊥DF,DG⊥DB,根據平面角的定義得出∠BDF是面DEF與面ABCD所成二面角的平面角,轉化到直角三角形求解即可.解法2:由PD⊥底面ABCD,所以 ![]() =(0,0,1)是平面ACDB的一個法向量;由(1)知,PB⊥平面DEF,所以
=(0,0,1)是平面ACDB的一個法向量;由(1)知,PB⊥平面DEF,所以 ![]() =(﹣λ,﹣1,1)是平面DEF的一個法向量.根據數量積得出夾角的余弦即可得出所求解的答案.
=(﹣λ,﹣1,1)是平面DEF的一個法向量.根據數量積得出夾角的余弦即可得出所求解的答案.


科目:高中數學 來源: 題型:
【題目】定義在R上的奇函數f(x),當x≥0時,f(x)= ![]() ,則關于x的函數F(x)=f(x)﹣a(0<a<1)的所有零點之和為( )
,則關于x的函數F(x)=f(x)﹣a(0<a<1)的所有零點之和為( )
A.3a﹣1
B.1﹣3a
C.3﹣a﹣1
D.1﹣3﹣a
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 上的一個最高點的坐標為
上的一個最高點的坐標為![]() ,由此點到相鄰最低點間的曲線與x軸交于點
,由此點到相鄰最低點間的曲線與x軸交于點![]() ,若
,若![]() .
.
(1)求![]() 的解析式.
的解析式.
(2)求![]() 在
在![]() 上的值域.
上的值域.
(3)若對任意實數![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知常數a>0,函數f(x)=ln(1+ax)﹣ ![]() .
.
(Ⅰ)討論f(x)在區間(0,+∞)上的單調性;
(Ⅱ)若f(x)存在兩個極值點x1 , x2 , 且f(x1)+f(x2)>0,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設a,b∈R,函數 ![]() ,g(x)=ex(e為自然對數的底數),且函數f(x)的圖象與函數g(x)的圖象在x=0處有公共的切線.
,g(x)=ex(e為自然對數的底數),且函數f(x)的圖象與函數g(x)的圖象在x=0處有公共的切線.
(Ⅰ)求b的值;
(Ⅱ)討論函數f(x)的單調性;
(Ⅲ)若g(x)>f(x)在區間(﹣∞,0)內恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax3+3x2+1,若至少存在兩個實數m,使得f(﹣m),f(1)、f(m+2)成等差數列,則過坐標原點作曲線y=f(x)的切線可以作( )
A.3條
B.2條
C.1條
D.0條
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com