【題目】一個袋中裝有形狀大小完全相同的球9個，其中紅球3個，白球6個，每次隨機取1個，直到取出3次紅球即停止．
(1)從袋中不放回地取球，求恰好取4次停止的概率P1；
(2)從袋中有放回地取球．
①求恰好取5次停止的概率P2；
②記5次之內(含5次)取到紅球的個數為
，求隨機變量
的分布列及數學期望．
【答案】(1) 
(2) ①
②
【解析】
試題分析：(1)從袋中不放回地取球，連續取4次，有
個不同的結果，由于是隨機取的，每個結果出現的可能性是相等的，恰好取4次停止，說明前三次有一次是白球，共有
個不同的結果，所以，根據古典概型的概率公式得
；
(2) 從袋中有放回地取球，每次取到紅球的概率
，取到白球的概率是
連續有放回地取
次，相當于
次獨立重復試驗；
①求恰好取5次停止的概率P2；說明前四次有兩次發生，第五次一定發生；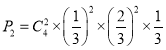
②記5次之內(含5次)取到紅球的個數為
，隨機變量
的所以可能取值集合是
由
次獨立重復試驗概率公式
即可求出隨機變量分布列，并由數學期望的公式計算出
.
試題解析：
解：(1)
4分
(2)①
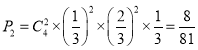6分
②隨機變量
的取值為
由次獨立重復試驗概率公式，得
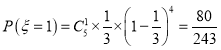
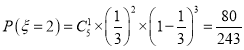
隨機變量
的分布列是
| 0 | 1 | 2 | 3 |
|
|
|
|
|
的數學期望是
12分
陽光課堂課時作業系列答案
鷹派教輔銜接教材河北教育出版社系列答案科目：高中數學 來源： 題型：
【題目】某班有學生50人，其中男同學30人，用分層抽樣的方法從該班抽取5人去參加某社區服務活動．
（1）求從該班男女同學在各抽取的人數；
（2）從抽取的5名同學中任選2名談此活動的感受，求選出的2名同學中恰有1名男同學的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
， 
，其中
…是然對數底數．
（1）若函數
有兩個不同的極值點
， 
，求實數
的取值范圍；
（2）當
時，求使不等式
在一切實數上恒成立的最大正整數
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若對任意
， 
有唯一確定的
與之對應，則稱
為關于
， 
的二元函數，現定義滿足下列性質的
為關于實數
， 
的廣義“距離”．
（
）非負性： 
，當且僅當
時取等號；
（
）對稱性： 
；
（
）三角形不等式： 
對任意的實數
均成立．
給出三個二元函數：①
；②
；③
，
則所有能夠成為關于
， 
的廣義“距離”的序號為__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知向量
=（2sinx，-1），
,函數f（x）=
．
（1）求函數f（x）的對稱中心；
（2）設△ABC的內角A，B，C所對的邊為a，b，c，且a2=bc，求f（A）的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖組合體中，三棱柱
的側面
是圓柱的軸截面（過圓柱的軸，截圓柱所得的截面），
是圓柱底面圓周上不與
，
重合的一個點.
（1）求證：無論點如何運動，平面
平面
；
（2）當點是弧
的中點時，求四棱錐
與圓柱的體積比．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
