
(本題14分)已知圓 和點
和點
(1)若過點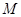 有且只有一條直線與圓
有且只有一條直線與圓 相切,求實數
相切,求實數 的值,并求出切線方程;
的值,并求出切線方程;
(2)若 ,過點
,過點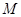 作圓的兩條弦
作圓的兩條弦 ,且
,且 互相垂直,求
互相垂直,求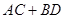 的最大值。
的最大值。
(1) 或即
或即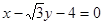 。(2)
。(2)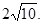
【解析】本試題主要是考查了直線與圓的位置關系的運用。
(1)因為圓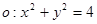 和點
和點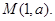 ,若過點
,若過點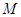 有且只有一條直線與圓
有且只有一條直線與圓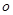 相切,則聯立方程組只有一個實數解得到切線方程。
相切,則聯立方程組只有一個實數解得到切線方程。
(2)若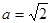 ,過點
,過點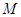 作圓的兩條弦
作圓的兩條弦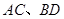 ,且
,且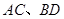 互相垂直,設
互相垂直,設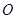 到直線
到直線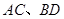 的距離分別為
的距離分別為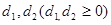 ,則
,則 于是
于是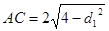 ,
,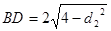 ,所以
,所以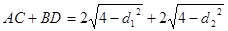 則
則 ,則利用不等式得到結論。
,則利用不等式得到結論。
解:(1)由條件知點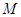 在圓
在圓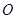 上,所以
上,所以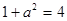 ,則
,則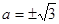 。當
。當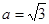 時,點
時,點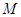 為
為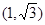 ,
,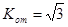 ,
,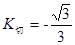 此時切線方程為
此時切線方程為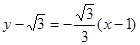 ,即
,即 。當
。當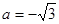 時,點
時,點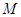 為
為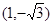 ,
,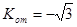 ,
, 此時切線方程為
此時切線方程為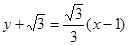 ,即
,即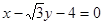 。所以所求的切線方程為
。所以所求的切線方程為 或即
或即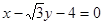 。-------------6分
。-------------6分
(2)設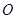 到直線
到直線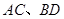 的距離分別為
的距離分別為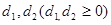 ,則
,則 于是
于是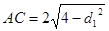 ,
,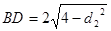 ,所以
,所以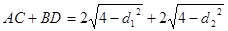 則
則 ,因為
,因為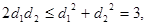 ,所以
,所以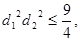 ,當且僅當
,當且僅當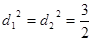 時取等號,所以
時取等號,所以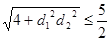 ,所以
,所以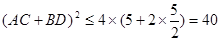 ,所以
,所以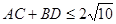 ,即
,即
的最大值為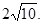 --------------------14分
--------------------14分


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:高中數學 來源: 題型:
(本題14分)已知直線![]() :y=kx+1與雙曲線C:2x2-y2=1的右支交于不同的兩點A、B。(1)求實數k的取值范圍;(2)是否存在實數k,使得以線段AB為直徑的圓經過雙曲線C的右焦點F?若薦在,求出k的值。若不存在,說明理由。
:y=kx+1與雙曲線C:2x2-y2=1的右支交于不同的兩點A、B。(1)求實數k的取值范圍;(2)是否存在實數k,使得以線段AB為直徑的圓經過雙曲線C的右焦點F?若薦在,求出k的值。若不存在,說明理由。
查看答案和解析>>
科目:高中數學 來源:2014屆廣東省高一年級第二學期5月月考數學試卷(解析版) 題型:解答題
(本題滿分14分)已知圓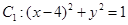 ,圓
,圓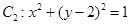 ,動點
,動點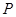 到圓
到圓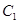 ,
,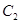 上點的距離的最小值相等.
上點的距離的最小值相等.
(1)求點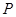 的軌跡方程;
的軌跡方程;
(2)點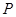 的軌跡上是否存在點
的軌跡上是否存在點 ,使得點
,使得點 到點
到點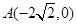 的距離減去點
的距離減去點 到點
到點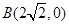 的距離的差為
的距離的差為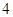 ,如果存在求出
,如果存在求出 點坐標,如果不存在說明理由.
點坐標,如果不存在說明理由.
查看答案和解析>>
科目:高中數學 來源:2013屆江蘇省淮安七校高二上學期期中考試理科數學 題型:解答題
(本題滿分14分)
已知圓 內有一點
內有一點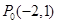 ,AB為過點
,AB為過點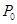 且傾斜角為α的弦,
且傾斜角為α的弦,
(1)當α=135º時,求直線AB的方程
(2)若弦AB被點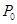 平分,求直線AB的方程。
平分,求直線AB的方程。
查看答案和解析>>
科目:高中數學 來源:2014屆廣東省湛江市高一第一學期第二學段考試數學 題型:解答題
(本題14分)已知與圓C: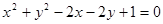 相切的直線
相切的直線 交x軸、y軸于A、B兩點,O為原點,|OA|=3,|OB|=b(b>2).
交x軸、y軸于A、B兩點,O為原點,|OA|=3,|OB|=b(b>2).
(1) 求b的值;
(2) 求△ABC的外接圓方程。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com