分析:(1)要證數列{an}是等比數列,只需證明數列{an}的后一項比前一項是常數即可,可先對y=x2求導數,y=x2在切點處的導數,就是在該點處的切線的斜率,求出切線方程,就可找到切點在x軸上的投影的橫坐標,再求相鄰橫坐標之商,看是否為常數,就可證出數列{an}是等比數列,再根據等比數列的通項公式求數列{an}的通項公式即可.
(2)根據(1)中所求數列{an}的通項公式求出數列{bn}的通項公式,再用錯位相減求前n項和Sn
解答:解:(1)對y=x
2求導數,得y'=2x,切點是M
n(a
n,a
n2)的切線方程是y-a
n2=2a
n(x-a
n).(2分)
當n=1時,切線過點P(1,0),即0-a
12=2a
1(1-a
1),得a
1=2;
當n>1時,切線過點
Pn-1(an-1,0),即0-=2an(an-1-an),得=2所以數列{a
n}是首項a
1=2,公比為2的等比數列.
所以數列{a
n}的通項公式為a
n=2
n,n∈N
*(6分)
(2)∵
bn=,a
n=2
n,∴
bn=S
n=
+
+
+…+
①
2S
n=
+
+…+
+
②
①-②,得-S
n=
+
+
+…+
-
=
-
=1-
-
=1-
點評:本題考查了等比數列的證明,以及錯位相減求和.



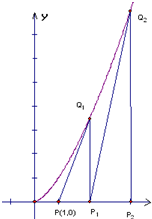 如圖,過點P(1,0)作曲線C:y=xk(x∈(0,+∞),k∈N*,k>1)的切線,切點為Q1,設Q1點在x軸上的投影是點P1;又過點P1作曲線C的切線,切點為Q2,設Q2在x軸上的投影是P2;…;依此下去,得到一系列點Q1,Q2,…,Qn,…,設點Qn的橫坐標為an.
如圖,過點P(1,0)作曲線C:y=xk(x∈(0,+∞),k∈N*,k>1)的切線,切點為Q1,設Q1點在x軸上的投影是點P1;又過點P1作曲線C的切線,切點為Q2,設Q2在x軸上的投影是P2;…;依此下去,得到一系列點Q1,Q2,…,Qn,…,設點Qn的橫坐標為an.

 (2009•錦州一模)過點P(1,0)作曲線C:y=x2(x>0)的切線,切點為Q1,沒Q1在x軸上的投影是P1,又過P1,作曲線C的切線,切點為Q2,設Q2在x軸上的投影是P2…,依次下去,得到一系列點Q1Q2,…Qn,設Qn的橫坐標為an.
(2009•錦州一模)過點P(1,0)作曲線C:y=x2(x>0)的切線,切點為Q1,沒Q1在x軸上的投影是P1,又過P1,作曲線C的切線,切點為Q2,設Q2在x軸上的投影是P2…,依次下去,得到一系列點Q1Q2,…Qn,設Qn的橫坐標為an.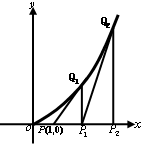 (2013•韶關二模)如圖,過點P(1,0)作曲線C:y=x2(x∈(0,+∞))的切線,切點為Q1,設點Q1在x軸上的投影是點P1;又過點P1作曲線C的切線,切點為Q2,設Q2在x軸上的投影是P2;…;依此下去,得到一系列點Q1,Q2,Q3-Qn,設點Qn的橫坐標為an.
(2013•韶關二模)如圖,過點P(1,0)作曲線C:y=x2(x∈(0,+∞))的切線,切點為Q1,設點Q1在x軸上的投影是點P1;又過點P1作曲線C的切線,切點為Q2,設Q2在x軸上的投影是P2;…;依此下去,得到一系列點Q1,Q2,Q3-Qn,設點Qn的橫坐標為an.