
【題目】已知函數f(x)![]() |2x﹣3|,g(x)
|2x﹣3|,g(x)![]() |2x+a+b|.
|2x+a+b|.
(1)解不等式f(x)![]() x2;
x2;
(2)當a![]() 0,b
0,b![]() 0時,若F(x)
0時,若F(x)![]() f(x)+g(x)的值域為[5,+∞),求證:
f(x)+g(x)的值域為[5,+∞),求證:![]() .
.
【答案】(1)![]() 或
或![]() ;(2)見解析
;(2)見解析
【解析】
(1)由題意可得|2x﹣3|![]() x2,由絕對值的意義,去絕對值,解不等式,求并集,可得所求解集;
x2,由絕對值的意義,去絕對值,解不等式,求并集,可得所求解集;
(2)由a![]() 0,b
0,b![]() 0,根據絕對值三角不等式,化簡可得F(x)的最小值,可得a+b的值,再由乘1法和基本不等式,即可得證.
0,根據絕對值三角不等式,化簡可得F(x)的最小值,可得a+b的值,再由乘1法和基本不等式,即可得證.
(1)解:不等式f(x)![]() x2化為|2x﹣3|
x2化為|2x﹣3|![]() x2,等價于
x2,等價于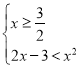 或
或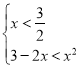 ,
,
即為![]() 或
或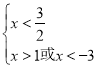 ,
,
解得x![]() 或x
或x![]() ﹣3或1
﹣3或1![]() x
x![]() ,
,
所以不等式f(x)![]() x2的解集為{x|x
x2的解集為{x|x![]() 1或x
1或x![]() ﹣3};
﹣3};
(2)證明:由a![]() 0,b
0,b![]() 0,
0,
根據絕對值三角不等式可知F(x)![]() f(x)+g(x)
f(x)+g(x)![]() |2x﹣3|+|2x+a+b|
|2x﹣3|+|2x+a+b|![]() |3﹣2x|+|2x+a+b|
|3﹣2x|+|2x+a+b|
≥|3﹣2x+2x+a+b|![]() |a+b+3|
|a+b+3|![]() a+b+3,
a+b+3,
又F(x)![]() f(x)+g(x)的值域為[5,+∞),
f(x)+g(x)的值域為[5,+∞),
可得a+b+3![]() 5,
5,
即a+b![]() 2,
2,
即(a+2)+(b+2)![]() 6,
6,
故![]() [(a+2)+(b+2)](
[(a+2)+(b+2)](![]() )
)
![]() (2
(2![]() )
)![]() (2+2
(2+2![]() )
)![]() ,
,
當且僅當![]() ,即a
,即a![]() b
b![]() 1時取等號時,
1時取等號時,
故![]() .
.


科目:高中數學 來源: 題型:
【題目】在黨中央的正確領導下,通過全國人民的齊心協力,特別是全體一線醫護人員的共同努力,新冠肺炎疫情得到了有效控制.作為集中醫學觀察隔離點的某酒店在疫情期間,為客人提供兩種速食品—“方便面”和“自熱米飯”.為調查這兩種速食品的受歡迎程度,酒店部門經理記錄了連續10天這兩種速食品的銷售量,得到如下頻數分布表(其中銷售量單位:盒):
第 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
方便面 | 103 | 93 | 98 | 93 | 106 | 86 | 87 | 94 | 91 | 99 |
自熱米飯 | 88 | 96 | 98 | 97 | 101 | 99 | 102 | 107 | 104 | 112 |
(1)根據兩組數據完成下面的莖葉圖(填到答題卡上);

(2)根據統計學知識,你認為哪種速食品更受歡迎,并簡要說明理由;
(3)求自熱米飯銷售量y關于天數t的線性回歸方程,并預估第12天自熱米飯的銷售量(結果精確到整數).
參考數據:![]() ,
,![]() .
.
附:回歸直線方程![]() ,其中
,其中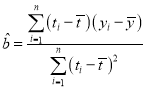 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在平面直角坐標系![]() 中,已知橢圓
中,已知橢圓![]() 的離心率為
的離心率為![]() ,
,![]() 為橢圓
為橢圓![]() 上位于第一象限上的點,
上位于第一象限上的點,![]() 為橢圓
為橢圓![]() 的上頂點,直線
的上頂點,直線![]() 與
與![]() 軸相交于點
軸相交于點![]() ,
,![]() ,
,![]() 的面積為
的面積為![]() .
.
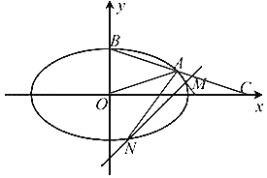
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)設直線![]() 過橢圓
過橢圓![]() 的右焦點,且與橢圓
的右焦點,且與橢圓![]() 相交于
相交于![]() 、
、![]() 兩點(
兩點(![]() 、
、![]() 在直線
在直線![]() 的同側),若
的同側),若![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在長方體ABCD﹣HKLE中,底面ABCD是邊長為3的正方形,對角線AC與BD相交于點O,點F在線段AH上,且![]() ,BE與底面ABCD所成角為
,BE與底面ABCD所成角為![]() .
.
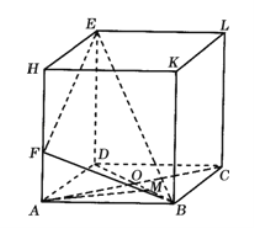
(1)求證:AC⊥BE;
(2)求二面角F﹣BE﹣D的余弦值;
(3)設點M在線段BD上,且AM//平面BEF,求DM的長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左右焦點分別為
的左右焦點分別為![]() ,
,![]() ,左頂點為
,左頂點為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,且
上,且![]() 的面積為
的面積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過原點![]() 且與
且與![]() 軸不重合的直線交橢圓
軸不重合的直線交橢圓![]() 于
于![]() ,
,![]() 兩點,直線
兩點,直線![]() 分別與
分別與![]() 軸交于點
軸交于點![]() ,
,![]() ,.求證:以
,.求證:以![]() 為直徑的圓恒過交點
為直徑的圓恒過交點![]() ,
,![]() ,并求出
,并求出![]() 面積的取值范圍.
面積的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,△ABC中,AB⊥BC,∠ACB=60°,D為AC中點,△ABD沿BD翻折過程中,直線AB與直線BC所成的最大角、最小角分別記為α1,β1,直線AD與直線BC所成最大角、最小角分別記為α2,β2,則有( )
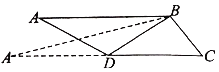
A.α1<α2,β1≤β2B.α1<α2,β1>β2
C.α1≥α2,β1≤β2D.α1≥α2,β1>β2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com