
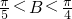 時,求△ABC的三邊長及角B(用反三角函數值表示);
時,求△ABC的三邊長及角B(用反三角函數值表示);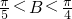 ,得
,得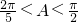 ,
,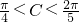 ,
,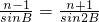 ,
,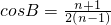 ,又
,又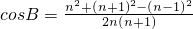 ,
, ,
,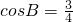 ,從而
,從而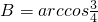 ;(10分)
;(10分)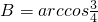 ,得到cosB=
,得到cosB= ,又B為銳角,
,又B為銳角,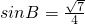 ,又a=6,c=5,
,又a=6,c=5, .(14分)
.(14分)

 鷹派教輔銜接教材河北教育出版社系列答案
鷹派教輔銜接教材河北教育出版社系列答案 初中暑期銜接系列答案
初中暑期銜接系列答案科目:高中數學 來源: 題型:
| π |
| 5 |
| π |
| 4 |
查看答案和解析>>
科目:高中數學 來源:盧灣區(qū)二模 題型:解答題
| π |
| 5 |
| π |
| 4 |
查看答案和解析>>
科目:高中數學 來源:2008年上海市盧灣區(qū)高考數學二模試卷(文理合卷)(解析版) 題型:解答題
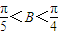 時,求△ABC的三邊長及角B(用反三角函數值表示);
時,求△ABC的三邊長及角B(用反三角函數值表示);查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com