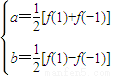若二次函數y=f(x)的圖象經過原點,且1≤f(-1)≤2,3≤f(1)≤4,求f(-2)的范圍.
【答案】
分析:法一,先根據要求設出二次函數,可以利用基本不等式性質變形找出f(2)解決;
法二,用數形結合思想,利用線性規劃的方法求解;
法三,利用方程思想反解a、b,利用f(-1)、f(1)來表示f(2)進而求解.
解答:解:因為y=f(x)的圖象經過原點,所以可設y=f(x)=ax
2+bx.于是
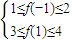
∴
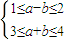
(I)
解法一(利用基本不等式的性質)
不等式組(Ⅰ)變形得
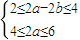
∴6≤4a-2b≤10,∴6≤f(-2)≤10,
所以f(-2)的取值范圍是[6,10].
解法二(數形結合)
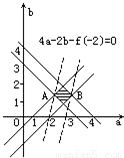
建立直角坐標系aob,作出不等式組(Ⅰ)所表示的區域,如圖中的陰影部分.
因為f(-2)=4a-2b,
所以4a-2b-f(-2)=0表示斜率為2的直線系.
如圖,當直線4a-2b-f(-2)=0過點A(2,1),B(3,1)時,
分別取得f(-2)的最小值6,最大值10.
即f(-2)的取值范圍是:6≤f(-2)≤10.
解法三(利用方程的思想)
∵
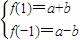
,∴
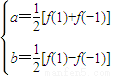
又f(-2)=4a-2b=3f(-1)+f(1),而
1≤f(-1)≤2,3≤f(1)≤4,①
所以3≤3f(-1)≤6.②
①+②得4≤3f(-1)+f(1)≤10,即6≤f(-2)≤10.
點評:本題考查不等式的應用,數形結合思想,線性規劃以及方程思想在本題中得到很好的體現,屬于基礎題.

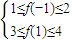 ∴
∴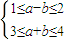 (I)
(I)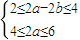

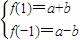 ,∴
,∴