
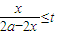 ,得 0<x≤
,得 0<x≤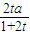 ,
,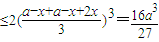 ,
,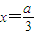 時等號成立.
時等號成立.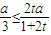 ,即
,即 ,
, ;
;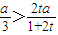 ,即
,即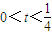 時,
時,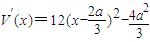 ,
,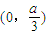 上單調遞減,
上單調遞減,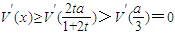 ,
,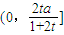 單調遞增,
單調遞增,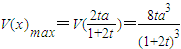
 ,則當
,則當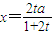 時,
時, ;
;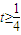 ,則當
,則當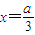 時,
時,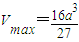 .
.

科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源:2011——2012學年湖北省洪湖二中高三八月份月考試卷理科數學 題型:解答題
(本題滿分12分)
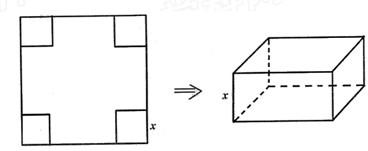
從邊長為2a的正方形鐵皮的四個角各截去一個邊長為x的小正方形,再將四邊向上折起,做成一個無蓋的長方體鐵盒,且要求長方體的高度x與底面正方形的邊長的比不超過常數t.
問:(1)求長方體的容積V關于x的函數表達式;(2)x取何值時,長方體的容積V有最大值?
查看答案和解析>>
科目:高中數學 來源:2010-2011學年湖北省、鐘祥一中高三第二次聯考數學理卷 題型:解答題
(12分)如圖,從邊長為2a的正方形鐵皮的四個角各截去一個邊長為x的小正方形,再將四邊向上折起,做成一個無蓋的長方體鐵盒,且要求長方體的高度x與底面正方形的邊長的比不超過常數t,問:x取何值時,長方體的容積V有最大值?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com