解:(1)函數f(x)在[-1,1]上單調增,證明如下
由題意,設x
1,x
2∈[-1,1],且x
1<x
2則x
1-x
2<0
∵x,y∈[-1,1],x+y≠0有(x+y)•[f(x)+f(y)]>0.
令x=x
1,y=-x
2,
∴f(x
1)+f(-x
2)<0
∵函數f(x)是定義在[-1,1]上的奇函數
∴f(x
1)-f(x
2)<0
∴函數f(x)在[-1,1]上單調增;
(2)由(1)知,
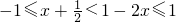
,解得:
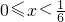
(3)由于函數f(x)在[-1,1]上單調增,
∴函數f(x)在[-1,1]上的最大值為f(1)=1
∴f(x)≤m
2-2am+1對所有x∈[-1,1],a∈[-1,1]恒成立可轉化為:0≤m
2-2am對所有a∈[-1,1]恒成立
∴
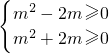
,
解得m≥2或m≤-2或m=0
分析:(1)設x
1,x
2∈[-1,1],且x
1<x
2,則x
1-x
2<0,利用x,y∈[-1,1],x+y≠0有(x+y)•[f(x)+f(y)]>0,可得f(x
1)+f(-x
2)<0,根據函數f(x)是定義在[-1,1]上的奇函數,即可得函數f(x)在[-1,1]上單調增;
(2)由(1)知,
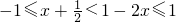
,解之即可;
(3)先確定函數f(x)在[-1,1]上的最大值為f(1)=1,將f(x)≤m
2-2am+1對所有x∈[-1,1],a∈[-1,1]恒成立轉化為:0≤m
2-2am對所有a∈[-1,1]恒成立,從而可求實數m的取值范圍.
點評:本題以抽象函數的性質為載體,考查函數的單調性,考查單調性與奇偶性的結合,同時考查了恒成立問題,解題的關鍵是:f(x)≤m
2-2am+1對所有x∈[-1,1],a∈[-1,1]恒成立轉化為:0≤m
2-2am對所有a∈[-1,1]恒成立

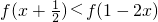 ;
;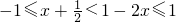 ,解得:
,解得: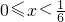
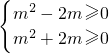 ,
,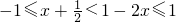 ,解之即可;
,解之即可;

 已知函數f(x)=x+
已知函數f(x)=x+