
【題目】如圖,在四棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() ,點
,點![]() 分別為
分別為![]() 的中點.
的中點.
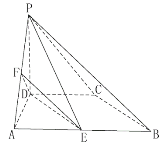
(1)求證:平面![]() 平面EFD;
平面EFD;
(2)求點![]() 到平面
到平面![]() 的距離.
的距離.
【答案】(1)詳見解析(2)![]()
【解析】
(1)根據面面平行的判定定理,在面EFD內找兩條相交直線平行于平面![]() ,即可證出;(2)根據等積法,
,即可證出;(2)根據等積法,![]() ,先求出三角形DEF的面積,再求出
,先求出三角形DEF的面積,再求出![]() ,即可求出點
,即可求出點![]() 到平面
到平面![]() 的距離。
的距離。
(1)由題意知:點![]() 是
是![]() 的中點,
的中點,![]() 且
且![]() ,
,
所以![]() ,所以四邊形
,所以四邊形![]() 是平行四邊形,則
是平行四邊形,則![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
又因為![]() 分別為
分別為![]() 的中點,所以
的中點,所以![]() .
.
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,所以
,所以![]()
因為平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]()
所以![]() 平面
平面![]() .
.
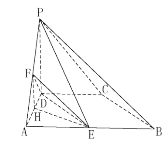
連![]() ,取
,取![]() 的中點
的中點![]() ,連
,連![]() ,易知
,易知![]() ,
,
![]() 平面
平面![]() 且
且![]() .
.
設點P到平面EFD的距離為d.
在Rt△![]() 中,
中,
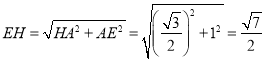
在Rt△![]() 中,
中,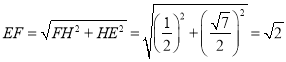
在Rt△![]() 中,
中,![]()
在Rt△![]() 中,
中,![]()
在△![]() 中,
中,![]() ,
,
即![]() ,
,
解得![]() ,
,
所以![]()
所以![]() .
.
因為平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,所以,
,所以,![]() 平面
平面![]() 所以,
所以,![]() 的長即是點
的長即是點![]() 到平面
到平面![]() 的距離.
的距離.
在Rt△![]() 中,
中,![]() ,
,
所以,![]() ,
,
所以![]() .
.
所以![]() ,
,
即![]() ,
,
即![]() ,解得
,解得![]() .
.
所以,點![]() 到平面
到平面![]() 的距離為
的距離為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某省高考改革實施方案指出:該省高考考生總成績將由語文、數學、外語3門統一高考成績和學生自主選擇的學業水平等級性考試科目共同構成.該省教育廳為了解正就讀高中的學生家長對高考改革方案所持的贊成態度,隨機從中抽取了100名城鄉家長作為樣本進行調查,調查結果顯示樣本中有25人持不贊成意見.下面是根據樣本的調查結果繪制的等高條形圖.
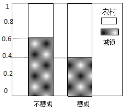
(1)根據已知條件與等高條形圖完成下面的2×2列聯表,并判斷我們能否有95%的把握認為“贊成高考改革方案與城鄉戶口有關”?
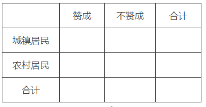
(2)利用分層抽樣從持“不贊成”意見家長中抽取5名參加學校交流活動,從中選派2名家長發言,求恰好有1名城鎮居民的概率.
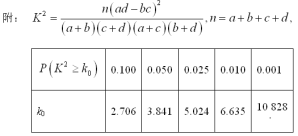
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國國際智能產業博覽會(智博會)每年在重慶市舉辦一屆,每年參加服務的志愿者分“嘉賓”、“法醫”等若干小組![]() 年底,來自重慶大學、西南大學、重慶醫科大學、西南政法大學的500名學生在重慶科技館多功能廳參加了“志愿者培訓”,如圖是四所大學參加培訓人數的不完整條形統計圖,現用分層抽樣的方法從中抽出50人作為2019年中國國際智博會服務的志愿者.
年底,來自重慶大學、西南大學、重慶醫科大學、西南政法大學的500名學生在重慶科技館多功能廳參加了“志愿者培訓”,如圖是四所大學參加培訓人數的不完整條形統計圖,現用分層抽樣的方法從中抽出50人作為2019年中國國際智博會服務的志愿者.
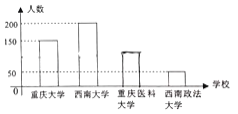
(1)若“嘉賓”小組需要2名志愿者,求這2人分別來自不同大學的概率(結果用分數表示)
(2)若“法醫”小組的3名志愿者只能從重慶醫科大學或西南政法大學抽出,用![]() 表示抽出志愿者來自重慶醫科大學的人數,求
表示抽出志愿者來自重慶醫科大學的人數,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 為實常數,函數
為實常數,函數![]() .
.
(1)當![]() 時,求
時,求![]() 的單調區間;
的單調區間;
(2)設![]() ,不等式
,不等式![]() 的解集為
的解集為![]() ,不等式
,不等式![]() 的解集為
的解集為![]() ,當
,當![]() 時,是否存在正整數
時,是否存在正整數![]() ,使得
,使得![]() 或
或![]() 成立.若存在,試找出所有的m;若不存在,請說明理由.
成立.若存在,試找出所有的m;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知動點![]() 到直線
到直線![]() 的距離比到定點
的距離比到定點![]() 的距離大1.
的距離大1.
(1)求動點![]() 的軌跡
的軌跡![]() 的方程.
的方程.
(2)若![]() 為直線
為直線![]() 上一動點,過點
上一動點,過點![]() 作曲線
作曲線![]() 的兩條切線
的兩條切線![]() ,
,![]() ,切點為
,切點為![]() ,
,![]() ,
,![]() 為
為![]() 的中點.
的中點.
①求證:![]() 軸;
軸;
②直線![]() 是否恒過一定點?若是,求出這個定點的坐標;若不是,請說明理由.
是否恒過一定點?若是,求出這個定點的坐標;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙、丙、丁四人進行一項益智游戲,方法如下:第一步:先由四人看著平面直角坐標系中方格內的16個棋子(如圖所示),甲從中記下某個棋子的坐標;第二步:甲分別告訴其他三人:告訴乙棋子的橫坐標.告訴丙棋子的縱坐標,告訴丁棋子的橫坐標與縱坐標相等;第三步:由乙、丙、丁依次回答.對話如下:“乙先說我無法確定.丙接著說我也無法確定.最后丁說我知道”.則甲記下的棋子的坐標為_____.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={1,2,3,4}和集合B={1,2,3,…,n},其中n≥5,![]() .從集合A中任取三個不同的元素,其中最小的元素用S表示;從集合B中任取三個不同的元素,其中最大的元素用T表示.記X=T-S.
.從集合A中任取三個不同的元素,其中最小的元素用S表示;從集合B中任取三個不同的元素,其中最大的元素用T表示.記X=T-S.
(1)當n=5時,求隨機變量X的概率分布和數學期望![]() ;
;
(2)求![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com