
【題目】某省高考改革實施方案指出:該省高考考生總成績將由語文、數學、外語3門統一高考成績和學生自主選擇的學業水平等級性考試科目共同構成.該省教育廳為了解正就讀高中的學生家長對高考改革方案所持的贊成態度,隨機從中抽取了100名城鄉家長作為樣本進行調查,調查結果顯示樣本中有25人持不贊成意見.下面是根據樣本的調查結果繪制的等高條形圖.
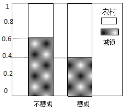
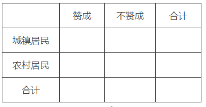
(1)根據已知條件與等高條形圖完成下面的2×2列聯表,并判斷我們能否有95%的把握認為“贊成高考改革方案與城鄉戶口有關”?
(2)利用分層抽樣從持“不贊成”意見家長中抽取5名參加學校交流活動,從中選派2名家長發言,求恰好有1名城鎮居民的概率.
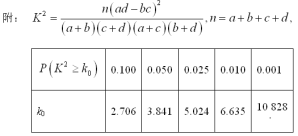
【答案】(1)沒有把握;(2)![]() .
.
【解析】
(1)根據所給數據以及等高條形圖可完成![]() 列聯表,利用公式求出
列聯表,利用公式求出![]() ,與臨界值比較即可得結論;(2)利用列舉法,確定基本事件的個數以及符合條件的事件數,再利用古典概型概率公式可求出恰好有1名城鎮居民的概率.
,與臨界值比較即可得結論;(2)利用列舉法,確定基本事件的個數以及符合條件的事件數,再利用古典概型概率公式可求出恰好有1名城鎮居民的概率.
(1)完成![]() 列聯表,如下:
列聯表,如下:
贊成 | 不贊成 | 合計 | |
城鎮居民 | 30 | 15 | 45 |
農村居民 | 45 | 10 | 55 |
合計 | 75 | 25 | 100 |
代入公式,得![]() 觀測值:
觀測值:
![]()
![]() 我們沒有
我們沒有![]() 的把握認為”贊成高考改革方案與城鄉戶口有關”.
的把握認為”贊成高考改革方案與城鄉戶口有關”.
(2)![]() 城鄉戶口與農村戶口比為
城鄉戶口與農村戶口比為![]() ,
,![]() 抽取5人中城鎮戶口的有3人,
抽取5人中城鎮戶口的有3人,
設為![]() ,農村戶口的有2人,設為
,農村戶口的有2人,設為![]() ,
,
5人選2人共有![]() ,10種選法,
,10種選法,
所以恰有1名城鎮居民的概率為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖,在矩形紙片![]() 中,
中,![]() ,
,![]() ,在線段
,在線段![]() 上取一點
上取一點![]() ,沿著過
,沿著過![]() 點的直線將矩形右下角折起,使得右下角頂點
點的直線將矩形右下角折起,使得右下角頂點![]() 恰好落在矩形的左邊
恰好落在矩形的左邊![]() 邊上.設折痕所在直線與
邊上.設折痕所在直線與![]() 交于
交于![]() 點,記折痕
點,記折痕![]() 的長度為
的長度為![]() ,翻折角
,翻折角![]() 為
為![]() .
.

(1)探求![]() 與
與![]() 的函數關系,推導出用
的函數關系,推導出用![]() 表示
表示![]() 的函數表達式;
的函數表達式;
(2)設![]() 的長為
的長為![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)確定點![]() 在何處時,翻折后重疊部分的圖形面積最小.
在何處時,翻折后重疊部分的圖形面積最小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的中心在原點,焦點在
的中心在原點,焦點在![]() 軸上,它的一個頂點恰好是拋物線
軸上,它的一個頂點恰好是拋物線![]() 的焦點,離心率等于
的焦點,離心率等于![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)過橢圓![]() 的右焦點
的右焦點![]() 作直線
作直線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點,交
兩點,交![]() 軸于
軸于![]() 點,若
點,若![]() ,
,![]() ,求證:
,求證:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】電子計算機誕生于20世紀中葉,是人類最偉大的技術發明之一.計算機利用二進制存儲信息,其中最基本單位是“位(bit)”,1位只能存放2種不同的信息:0或l,分別通過電路的斷或通實現.“字節(Byte)”是更大的存儲單位,1Byte=8bit,因此1字節可存放從00000000(2)至11111111(2)共256種不同的信息.將這256個二進制數中,所有恰有相鄰兩位數是1其余各位數均是0的所有數相加,則計算結果用十進制表示為
A. 254B. 381C. 510D. 765
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于無窮數列![]() ,“若存在
,“若存在![]() ,必有
,必有![]() ”,則稱數列
”,則稱數列![]() 具有
具有![]() 性質.
性質.
(1)若數列![]() 滿足
滿足 ,判斷數列
,判斷數列![]() 是否具有
是否具有![]() 性質?是否具有
性質?是否具有![]() 性質?
性質?
(2)對于無窮數列![]() ,設
,設![]() ,求證:若數列
,求證:若數列![]() 具有
具有![]() 性質,則
性質,則![]() 必為有限集;
必為有限集;
(3)已知![]() 是各項均為正整數的數列,且
是各項均為正整數的數列,且![]() 既具有
既具有![]() 性質,又具有
性質,又具有![]() 性質,是否存在正整數
性質,是否存在正整數![]() ,
,![]() ,使得
,使得![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…成等差數列.若存在,請加以證明;若不存在,說明理由.
,…成等差數列.若存在,請加以證明;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知關于x的不等式m-|x-2|≥1,其解集為[0,4].
(1)求m的值;
(2)若a,b均為正實數,且滿足a+b=m,求a2+b2的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com