
已知函數 的導函數
的導函數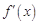 是二次函數,當
是二次函數,當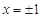 時,
時, 有極值,且極大值為2,
有極值,且極大值為2,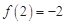 .
.
(1)求函數 的解析式;
的解析式;
(2)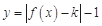 有兩個零點,求實數
有兩個零點,求實數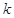 的取值范圍;
的取值范圍;
(3)設函數 ,若存在實數
,若存在實數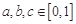 ,使得
,使得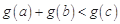 ,求
,求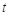 的取值范圍.
的取值范圍.
(1)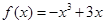 ;(2)
;(2)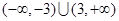 ;(3)
;(3) .
.
解析試題分析:(1)先通過函數 的導函數
的導函數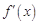 是二次函數,且當
是二次函數,且當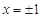 時,
時, 有極值將函數
有極值將函數 的導函數設出來:
的導函數設出來: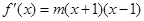 .從而可設
.從而可設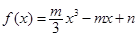 ,其中
,其中 為常數.再由
為常數.再由 極大值為2及
極大值為2及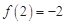 將
將 求出.注意,
求出.注意, 極大值為2,即
極大值為2,即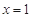 或
或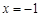 時,函數值為2.結合
時,函數值為2.結合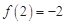 正好可以將其中一種情況舍去,從而解出
正好可以將其中一種情況舍去,從而解出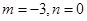 ,于是得到函數
,于是得到函數 的解析式;(2)由
的解析式;(2)由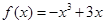 ,
, 列出表格,分析函數
列出表格,分析函數 的單調性和極值.
的單調性和極值.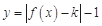 有兩個零點,即方程
有兩個零點,即方程 有兩個根,而
有兩個根,而 ,即方程
,即方程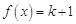 與方程
與方程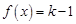 各只有一個解.結合函數
各只有一個解.結合函數 的單調性和極值,發現方程
的單調性和極值,發現方程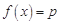 只有當
只有當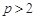 或
或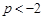 時才只有一個解.所以有
時才只有一個解.所以有 或
或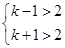 或
或 ,從而解得
,從而解得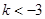 或
或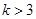 ;(3)由于存在實數
;(3)由于存在實數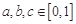 ,使得
,使得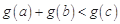 ,也就是說
,也就是說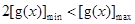 ,否則就不存在實數
,否則就不存在實數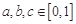 ,使得
,使得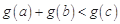 .因此本題轉化為求
.因此本題轉化為求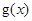 在
在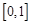 上的最大值與最小值.根據條件可得
上的最大值與最小值.根據條件可得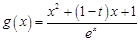 ,所以其導函數
,所以其導函數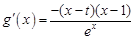 .然后討論
.然后討論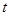 的范圍以得到
的范圍以得到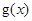 在
在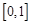 上單調性,從而找出最值.再通過不等式
上單調性,從而找出最值.再通過不等式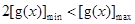 得到
得到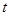 的取值范圍.注意當
的取值范圍.注意當 時比較麻煩,
時比較麻煩,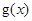 在
在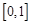 上先減后增,
上先減后增,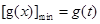 ,而最大值無法確定是
,而最大值無法確定是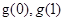 中的哪一個,所以我們用
中的哪一個,所以我們用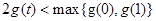 來表示不等式
來表示不等式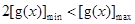 .
.
試題解析:(1)由條件,可設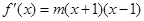 ,則
,則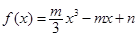 ,其中
,其中 為常數.
為常數.
因為 極大值為2.所以
極大值為2.所以 或
或 ,即
,即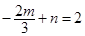 或
或 .由
.由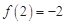 得
得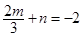 ①.所以
①.所以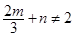 ,即
,即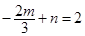 ②.由①②可得,
②.由①②可得,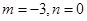 .所以
.所以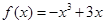 .
.
(2)由(1),得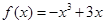 ,即
,即 .列表:
.列表: