
在平面直角坐標(biāo)系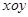 中,已知圓心在
中,已知圓心在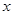 軸上,半徑為
軸上,半徑為 的圓
的圓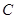 位于
位于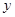 軸的右側(cè),且與
軸的右側(cè),且與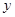 軸相切,
軸相切,
(Ⅰ)求圓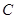 的方程;
的方程;
(Ⅱ)若橢圓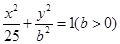 的離心率為
的離心率為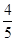 ,且左右焦點為
,且左右焦點為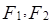 ,試探究在圓
,試探究在圓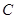 上是否存在點
上是否存在點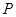 ,使得
,使得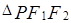 為直角三角形?若存在,請指出共有幾個這樣的
為直角三角形?若存在,請指出共有幾個這樣的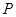 點?并說明理由(不必具體求出這些點的坐標(biāo))
點?并說明理由(不必具體求出這些點的坐標(biāo))
(Ⅰ)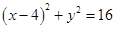 ;(Ⅱ),圓
;(Ⅱ),圓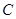 上存在4個點
上存在4個點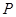 ,使得
,使得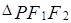 為直角三角形.
為直角三角形.
【解析】
試題分析:(Ⅰ)求圓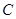 的方程,只要求出圓心與半徑即可,而已知圓
的方程,只要求出圓心與半徑即可,而已知圓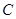 的半徑為
的半徑為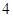 ,圓心在
,圓心在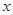 軸上,圓
軸上,圓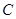 位于
位于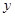 軸的右側(cè),且與
軸的右側(cè),且與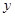 軸相切,故圓心為
軸相切,故圓心為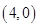 ,從而可得圓
,從而可得圓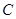 的方程;(Ⅱ)探究在圓
的方程;(Ⅱ)探究在圓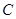 上是否存在點
上是否存在點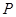 ,使得
,使得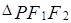 為直角三角形,首先求出
為直角三角形,首先求出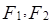 的坐標(biāo),而
的坐標(biāo),而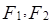 是橢圓
是橢圓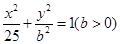 的左右焦點,須求出橢圓的方程,由題意橢圓
的左右焦點,須求出橢圓的方程,由題意橢圓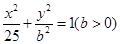 的離心率為
的離心率為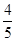 ,
,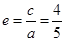 ,可求得,
,可求得, ,可得
,可得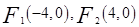 ,
,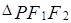 為直角三角形,有圓的方程可知,只需過
為直角三角形,有圓的方程可知,只需過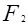 作
作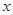 軸的垂線,與圓的兩個交點符合題意,過
軸的垂線,與圓的兩個交點符合題意,過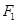 可作圓的兩條切線,與圓的兩個切點也符合,從而找到
可作圓的兩條切線,與圓的兩個切點也符合,從而找到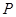 點.
點.
試題解析:(Ⅰ)依題意,設(shè)圓的方程為(x-a)2+y2=16(a>0). (1分)
∵圓與y軸相切,∴a=4,∴圓的方程為(x-4)2+y2=16 (4分)
(Ⅱ)∵橢圓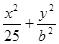 =1的離心率為
=1的離心率為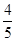 ,∴e=
,∴e=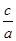 =
=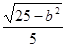 =
=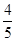
解得b2=9 (6分)
∴c=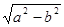 =4,∴F1(-4,0),F2(4,0)
(7分)
=4,∴F1(-4,0),F2(4,0)
(7分)
∴F2(4,0)恰為圓心C (8分)
(i)過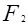 作
作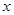 軸的垂線,交圓P1,P2,則∠P1F2F1=∠P2F2F1=90°,符合題意;(10分)
軸的垂線,交圓P1,P2,則∠P1F2F1=∠P2F2F1=90°,符合題意;(10分)
(ii)過F1可作圓的兩條切線,分別與圓相切于點P3,P4,
連接CP3,CP4,則∠F1P3F2=∠F1P4F2=90°,符合題意. (12分)
綜上,圓C上存在4個點P,使得△PF1F2為直角三角形. (13分)
考點:圓的方程,橢圓方程,探索性問題.


科目:高中數(shù)學(xué) 來源: 題型:
| π | 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| π |
| 2 |
| 3π |
| 2 |
| AC |
| BC |
| π |
| 2 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com