
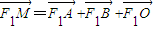 (其中O為坐標原點),求點M的軌跡方程;
(其中O為坐標原點),求點M的軌跡方程;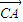 •
•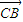 為常數?若存在,求出點C的坐標;若不存在,請說明理由.
為常數?若存在,求出點C的坐標;若不存在,請說明理由.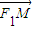 ,
,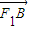 ,
,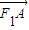 ,
,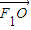 ,根據
,根據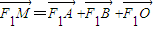 可得到x1,x2,x以及y1,y2,y的關系,即可表示出AB的中點坐標,然后分AB不與x軸垂直和AB與x軸垂直兩種情況進行討論.
可得到x1,x2,x以及y1,y2,y的關系,即可表示出AB的中點坐標,然后分AB不與x軸垂直和AB與x軸垂直兩種情況進行討論.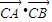 為常數,當AB不與x軸垂直時,設出直線AB的方程,然后與雙曲線方程聯立消去y得到關于x的一元二次方程,進而可得到兩根之和與兩根之積,表示出向量
為常數,當AB不與x軸垂直時,設出直線AB的方程,然后與雙曲線方程聯立消去y得到關于x的一元二次方程,進而可得到兩根之和與兩根之積,表示出向量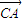 •
•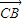 并將所求的兩根之和與兩根之積代入整理即可求出C的坐標;當AB與x軸垂直時可直接得到A,B的坐標,再由
并將所求的兩根之和與兩根之積代入整理即可求出C的坐標;當AB與x軸垂直時可直接得到A,B的坐標,再由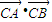 =-1,可確定答案.
=-1,可確定答案.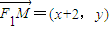 ,
,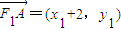 ,
,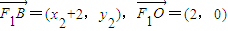 ,
,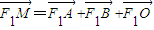 ,得
,得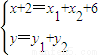 ,即
,即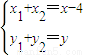 ,
,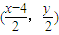 ,
,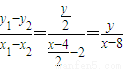 ,即
,即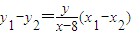 ,
,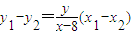 代入上式,化簡得(x-6)2-y2=4,
代入上式,化簡得(x-6)2-y2=4,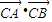 為常數,
為常數,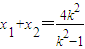 ,
,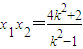 ,
,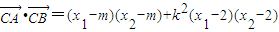
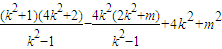
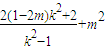
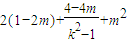 .
.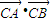 是與k無關的常數,所以4-4m=0,即m=1,此時
是與k無關的常數,所以4-4m=0,即m=1,此時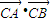 =-1,
=-1,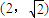 ,
,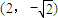 ,
,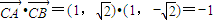 ,
,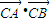 為常數.
為常數.

科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| F1M |
| F1A |
| F1B |
| F1O |
查看答案和解析>>
科目:高中數學 來源: 題型:
| A、tanα+tanβ+tanγ=0 | B、tanα+tanβ-tanγ=0 | C、tanα+tanβ+2tanγ=0 | D、tanα+tanβ-2tanγ=0 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com