
【題目】已知函數f(x)的定義域為{x|x∈R,且x≠0},對定義域內的任意x1、x2,都有f(x1·x2)=f(x1)+f(x2),且當x>1時,f(x)>0.
(1)求證:f(x)是偶函數;
(2)求證:f(x)在(0,+∞)上是增函數.
【答案】(1)見解析 (2)見解析
【解析】證明: (1)因對定義域內的任意x1、x2都有
f(x1·x2)=f(x1)+f(x2),
令x1=x,x2=-1,
則有f(-x)=f(x)+f(-1).
又令x1=x2=-1,得2f(-1)=f(1).
再令x1=x2=1,得f(1)=0,
從而f(-1)=0,
于是有f(-x)=f(x),所以f(x)是偶函數.
(2)設0<x1<x2,
則f(x1)-f(x2)=f(x1)-f(x1·![]() )=f(x1)-[f(x1)+f(
)=f(x1)-[f(x1)+f(![]() )]=-f(
)]=-f(![]() ),
),
由于0<x1<x2,所以![]() >1,從而f(
>1,從而f(![]() )>0,
)>0,
故f(x1)-f(x2)<0,即f(x1)<f(x2),
所以f(x)在(0,+∞)上是增函數.


科目:高中數學 來源: 題型:
【題目】數列{an}滿足a1= ![]() ,an+1﹣1=an(an﹣1)(n∈N*)且Sn=
,an+1﹣1=an(an﹣1)(n∈N*)且Sn= ![]() +
+ ![]() +…+
+…+ ![]() ,則Sn的整數部分的所有可能值構成的集合是( )
,則Sn的整數部分的所有可能值構成的集合是( )
A.{0,1,2}
B.{0,1,2,3}
C.{1,2}
D.{0,2}
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設集合A=[0, ![]() ),B=[
),B=[ ![]() ,1],函數f (x)=
,1],函數f (x)= 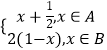 ,若x0∈A,且f[f (x0)]∈A,則x0的取值范圍是( )
,若x0∈A,且f[f (x0)]∈A,則x0的取值范圍是( )
A.(0, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.( ![]() ,
, ![]() )
)
D.[0, ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)是定義在(﹣∞,+∞)上的偶函數,且它在[0,+∞)上單調遞增,若a=f( ![]() ),b=f(
),b=f( ![]() ),c=f(﹣2),則a,b,c的大小關系是(從小到大排)
),c=f(﹣2),則a,b,c的大小關系是(從小到大排)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知AB是⊙O的直徑,點D是⊙O上一點,過點D作⊙O的切線,交AB的延長線于點C,過點C作AC的垂線,交AD的延長線于點E. 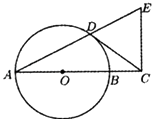
(1)求證:△CDE為等腰三角形;
(2)若AD=2, ![]() =
= ![]() ,求⊙O的面積.
,求⊙O的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定橢圓![]() ,稱圓
,稱圓![]() 為橢圓
為橢圓![]() 的“伴隨圓”.已知點
的“伴隨圓”.已知點![]() 是橢圓
是橢圓![]() 上的點
上的點
(1)若過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 有且只有一個公共點,求
有且只有一個公共點,求![]() 被橢圓
被橢圓![]() 的伴隨圓
的伴隨圓![]() 所截得的弦長:
所截得的弦長:
(2)![]() 是橢圓
是橢圓![]() 上的兩點,設
上的兩點,設![]() 是直線
是直線![]() 的斜率,且滿足
的斜率,且滿足![]() ,試問:直線
,試問:直線![]() 是否過定點,如果過定點,求出定點坐標,如果不過定點,試說明理由。
是否過定點,如果過定點,求出定點坐標,如果不過定點,試說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com