Question

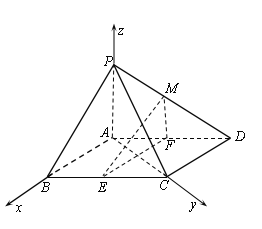
【題目】如圖，在四棱錐P﹣ABCD中，底面ABCD是平行四邊形，∠BCD=135°，側面PAB⊥底面ABCD，∠BAP=90°，AB=AC=PA=2，E，F分別為BC，AD的中點，點M在線段PD上．

（Ⅰ）求證：EF⊥平面PAC；

（Ⅱ）若M為PD的中點，求證：ME∥平面PAB；

（Ⅲ）如果直線ME與平面PBC所成的角和直線ME與平面ABCD所成的角相等，求的值．

Answer 1

【答案】（Ⅰ）見解析；（Ⅱ）見解析；（Ⅲ）

【解析】

試題分析：由平行四邊形的性質可得，即，由面面垂直的性質得出平面，故，從而平面

以為原點建立空間直角坐標系，設，，求出平面，平面的法向量以及的坐標，根據線面角相等列方程求解即可得到答案

解析：(1）證明：在平行四邊形中，因為，，

所以．由分別為的中點，得， 所以．

因為側面底面，且，所以底面．

又因為底面，所以．

又因為，平面，平面，所以平面．

（2）解：因為底面，，所以兩兩

垂直，以分別為、、，建立空間直角坐標系，則

，

所以，，，

設，則，

所以，，易得平面

的法向量．

設平面的法向量為，由，，得 令， 得．

因為直線與平面所成的角和此直線與平面所成的角相等，

所以，即，所以 ，

解得，或（舍）． 綜上所得：