【答案】
分析:化簡ω,利用

,求出θ的三角函數值,再用
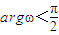
,來驗證ω,從而求出θ的值.
解答:解法一
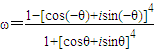
=
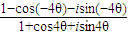
=

=tg2θ(sin4θ+icos4θ).
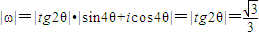
,
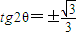
.
因0<θ<π,故有
(ⅰ)當
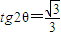
時,得
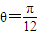
或

,這時都有
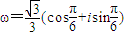
,
得
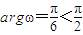
,適合題意.
(ⅱ)當
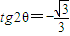
時,得
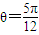
或
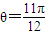
,這時都有

,
得
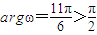
,不適合題意,舍去.
綜合(ⅰ)、(ⅱ)知
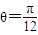
或
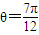
.
解法二z
4=cos4θ+isin4θ.
記φ=4θ,得

.

.=
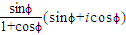
=
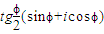
.∵

,
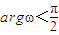
,
①②③
∴

當①成立時,②恒成立,所以θ應滿足
(ⅰ)

,或(ⅱ)
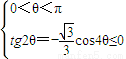
,
解(ⅰ)得

或
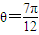
.(ⅱ)無解.
綜合(ⅰ)、(ⅱ)
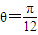
或
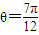
.
點評:本題考查復數的基本概念和運算,三角函數式的恒等變形及綜合解題能力;注意分類討論思想的應用,難度較大.

 ,并且
,并且 ,
, ,求θ.
,求θ.