
【題目】如圖,在三棱柱![]() 中,底面
中,底面![]() 為正三角形,側(cè)棱
為正三角形,側(cè)棱![]() 底面
底面![]() .已知
.已知![]() 是
是![]() 的中點(diǎn),
的中點(diǎn), ![]() .
.

(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求證:![]() ∥平面
∥平面![]() ;
;
(Ⅲ)求三棱錐![]() 的體積.
的體積.
【答案】(Ⅰ)見解析 (Ⅱ)見解析(Ⅲ)![]()
【解析】試題分析:(Ⅰ)由![]() ,
, ![]() 及
及![]() ,可證
,可證![]() 平面
平面![]() .即可證明
.即可證明
平面![]() 平面
平面![]() ;
;
(Ⅱ)證明![]() .又因?yàn)?/span>
.又因?yàn)?/span>![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() ∥平面
∥平面![]()
(Ⅲ)由![]() 即可求得三棱錐
即可求得三棱錐![]() 的體積.
的體積.
試題解析:
(Ⅰ)證明:由已知![]() 為正三角形,且D是BC的中點(diǎn),
為正三角形,且D是BC的中點(diǎn),
所以![]() .
.
因?yàn)閭?cè)棱![]() 底面
底面![]() ,
, ![]() ,
,
所以![]() 底面
底面![]() .
.
又因?yàn)?/span>![]() 底面
底面![]() ,所以
,所以![]() .
.
而![]() ,
,
所以![]() 平面
平面![]() .
.
因?yàn)?/span>![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(Ⅱ)證明:連接![]() ,設(shè)
,設(shè)![]() ,連接
,連接![]() .
.
由已知得,四邊形![]() 為正方形,則
為正方形,則![]() 為
為![]() 的中點(diǎn).
的中點(diǎn).
因?yàn)?/span>![]() 是
是![]() 的中點(diǎn),所以
的中點(diǎn),所以![]() .
.
又因?yàn)?/span>![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() ∥平面
∥平面![]()
(Ⅲ)由(Ⅱ)可知![]() ∥平面
∥平面![]() ,
,
所以![]() 與
與![]() 到平面
到平面![]() 的距離相等,
的距離相等,
所以![]() .
.
由題設(shè)及![]() ,得
,得![]() ,且
,且![]() .
.
所以![]() ,
,
所以三棱錐![]() 的體積為
的體積為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)數(shù)列![]() 滿足
滿足![]() ,其中
,其中![]() ,且
,且![]() ,
, ![]() 為常數(shù).
為常數(shù).
(1)若![]() 是等差數(shù)列,且公差
是等差數(shù)列,且公差![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,且存在
,且存在![]() ,使得
,使得![]() 對任意的
對任意的![]() 都成立,求
都成立,求![]() 的最小值;
的最小值;
(3)若![]() ,且數(shù)列
,且數(shù)列![]() 不是常數(shù)列,如果存在正整數(shù)
不是常數(shù)列,如果存在正整數(shù)![]() ,使得
,使得![]() 對任意的
對任意的![]() 均成立. 求所有滿足條件的數(shù)列
均成立. 求所有滿足條件的數(shù)列![]() 中
中![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,點(diǎn)
中,點(diǎn)![]() ,圓
,圓![]() ,以動點(diǎn)
,以動點(diǎn)![]() 為圓心的圓經(jīng)過點(diǎn)
為圓心的圓經(jīng)過點(diǎn)![]() ,且圓
,且圓![]() 與圓
與圓![]() 內(nèi)切.
內(nèi)切.
(Ⅰ)求動點(diǎn)![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)若直線![]() 過點(diǎn)
過點(diǎn)![]() ,且與曲線
,且與曲線![]() 交于
交于![]() 兩點(diǎn),則在
兩點(diǎn),則在![]() 軸上是否存在一點(diǎn)
軸上是否存在一點(diǎn)![]() ,使得
,使得![]() 軸平分
軸平分![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】煉鋼是一個(gè)氧化降碳的過程,鋼水含碳量的多少直接影響冶煉時(shí)間的長短,必須掌握鋼水含碳量和冶煉時(shí)間的關(guān)系.如果已測得爐料溶化完畢時(shí)鋼水的含碳量x與冶煉時(shí)間y(從爐料溶化完畢到出鋼的時(shí)間)的一組數(shù)據(jù),如表所示:
x(0.01%) | 104 | 180 | 190 | 177 | 147 | 134 | 150 | 191 | 204 | 121 |
y/min | 100 | 200 | 210 | 185 | 155 | 135 | 170 | 205 | 235 | 125 |
(1)y與x是否具有線性相關(guān)關(guān)系?
(2)如果y與x具有線性相關(guān)關(guān)系,求回歸直線方程.
(3)預(yù)報(bào)當(dāng)鋼水含碳量為160個(gè)0.01%時(shí),應(yīng)冶煉多少分鐘?
參考公式:r=![]()
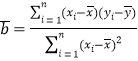 ,
,
線性回歸方程![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() 為參數(shù)),在以原點(diǎn)為極點(diǎn),
為參數(shù)),在以原點(diǎn)為極點(diǎn), ![]() 軸正半軸為極軸的極坐標(biāo)系中,直線
軸正半軸為極軸的極坐標(biāo)系中,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的傾斜角;
的傾斜角;
(2)設(shè)點(diǎn)![]() 和
和![]() 交于
交于![]() 兩點(diǎn),求
兩點(diǎn),求![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】【2018屆山西省太原十二中高三上學(xué)期1月月考】運(yùn)動員甲在最近![]() 場
場![]() 比賽中所得分?jǐn)?shù)的莖葉圖如圖所示,由于疏忽,莖葉圖中的兩個(gè)數(shù)據(jù)上出行了污漬,導(dǎo)致這兩個(gè)數(shù)字無法辨認(rèn),但統(tǒng)計(jì)員記得除掉污漬
比賽中所得分?jǐn)?shù)的莖葉圖如圖所示,由于疏忽,莖葉圖中的兩個(gè)數(shù)據(jù)上出行了污漬,導(dǎo)致這兩個(gè)數(shù)字無法辨認(rèn),但統(tǒng)計(jì)員記得除掉污漬![]() 處的數(shù)字不影響整體中位數(shù),且這六個(gè)數(shù)據(jù)的平均值為
處的數(shù)字不影響整體中位數(shù),且這六個(gè)數(shù)據(jù)的平均值為![]() .
.
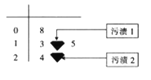
(1)求污漬![]() 處的數(shù)字;
處的數(shù)字;
(2)籃球運(yùn)動員乙在最近![]() 場
場![]() 的比賽中所得分?jǐn)?shù)為
的比賽中所得分?jǐn)?shù)為![]() .試分別以各自
.試分別以各自![]() 場比賽得分的平均數(shù)與方差來分析這兩名籃球運(yùn)動員的發(fā)揮水平.
場比賽得分的平均數(shù)與方差來分析這兩名籃球運(yùn)動員的發(fā)揮水平.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,且
,且![]() ,
,![]() .四邊形
.四邊形![]() 滿足
滿足![]() ,
,![]() ,
,![]() .
.![]() 為側(cè)棱
為側(cè)棱![]() 的中點(diǎn),
的中點(diǎn),![]() 為側(cè)棱
為側(cè)棱![]() 上的任意一點(diǎn).
上的任意一點(diǎn).
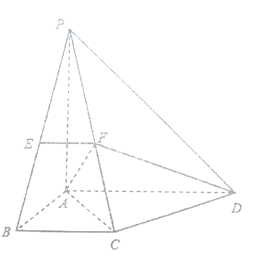
(1)若![]() 為
為![]() 的中點(diǎn),求證: 面
的中點(diǎn),求證: 面![]() 平面
平面![]() ;
;
(2)是否存在點(diǎn)![]() ,使得直線
,使得直線![]() 與平面
與平面![]() 垂直? 若存在,寫出證明過程并求出線段
垂直? 若存在,寫出證明過程并求出線段![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱柱![]() 中,底面
中,底面![]() 是邊長為2的等邊三角形,平面
是邊長為2的等邊三角形,平面![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,且
,且![]() 平面
平面![]() .
.

(1)求證: ![]() ;
;
(2)若四邊形![]() 是正方形,且
是正方形,且![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)數(shù)列{an}的前n項(xiàng)和為Sn,且Sn=4an﹣p,其中p是不為零的常數(shù).
(1)證明:數(shù)列{an}是等比數(shù)列;
(2)當(dāng)p=3時(shí),若數(shù)列{bn}滿足bn+1=bn+an(n∈N*),b1=2,求數(shù)列{bn}的通項(xiàng)公式.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com