
【題目】如圖已知四棱錐P﹣ABCD的底面ABCD是邊長為2的正方形,PD⊥底面ABCD,E,F分別為棱BC,AD的中點. 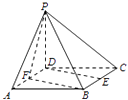
(1)若PD=1,求異面直線PB和DE所成角的余弦值.
(2)若二面角P﹣BF﹣C的余弦值為 ![]() ,求四棱錐P﹣ABCD的體積.
,求四棱錐P﹣ABCD的體積.
【答案】
(1)證明:E,F分別為棱BC,AD的中點,ABCD是邊長為2的正方形
∴DF∥BE且DF=BE
∴DFBE為平行四邊形
∴DE∥BF
∴∠PBF是PB與DE的所成角
△PBF中,BF= ![]() ,PF=,
,PF=, ![]() ,PB=3,
,PB=3,
∴cos∠PBF= ![]() ,
,
∴異面直線PB和DE所成角的余弦值為 ![]() ;
;
(2)解:如圖,以D為原點,射線DA,DC,DP分別為x,y,z軸建立空間直角坐標系.設PD=a,
可得如下點的坐標:
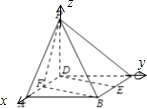
P(0,0,a),F(1,0,0),B(2,2,0)
則有: ![]() =(1,0,﹣a),
=(1,0,﹣a), ![]() =(1,2,0)
=(1,2,0)
因為PD⊥底面ABCD,所以平面ABCD的一個法向量為 ![]() =(0,0,1)
=(0,0,1)
設平面PFB的一個法向量為 ![]() =(x,y,z),則可得
=(x,y,z),則可得 ![]() ,令x=1,得z=
,令x=1,得z= ![]() ,y=﹣
,y=﹣ ![]() ,
,
所以 ![]() =(1,﹣
=(1,﹣ ![]() ,
, ![]() )
)
由已知,二面角P﹣BF﹣C的余弦值為 ![]() ,所以得
,所以得 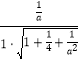 =
= ![]() ,解得a=2.
,解得a=2.
因為PD是四棱錐P﹣ABCD的高,
所以其體積為VP﹣ABCD= ![]() ×2×4=
×2×4= ![]() .
.
【解析】(1)根據一對對邊平行且相等,得到一個四邊形是平行四邊形,根據平行四邊形對邊平行,把兩條異面直線所成的角表示出來,放到△PBF中,利用余弦定理求出角的余弦值.(2)以D為原點,射線DA,DC,DP分別為x,y,z軸建立空間直角坐標系,設出線段的長,根據條件中所給的兩個平面的二面角的值,求出設出的a的值,再求出四棱錐的體積.
【考點精析】本題主要考查了異面直線及其所成的角的相關知識點,需要掌握異面直線所成角的求法:1、平移法:在異面直線中的一條直線中選擇一特殊點,作另一條的平行線;2、補形法:把空間圖形補成熟悉的或完整的幾何體,如正方體、平行六面體、長方體等,其目的在于容易發現兩條異面直線間的關系才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】甲、乙兩位小學生各有2008年奧運吉祥物“福娃”5個(其中“貝貝”、“晶晶”、“歡歡”、“迎迎”和“妮妮各一個”),現以投擲一個骰子的方式進行游戲,規則如下:當出現向上的點數是奇數時,甲贏得乙一個福娃;否則乙贏得甲一個福娃,規定擲骰子的次數達9次時,或在此前某人已贏得所有福娃時游戲終止.記游戲終止時投擲骰子的次數為ξ
(1)求擲骰子的次數為7的概率;
(2)求ξ的分布列及數學期望Eξ.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【選修4-4:坐標系與參數方程】
在直角坐標系![]() 中圓C的參數方程為
中圓C的參數方程為![]() (
(![]() 為參數),以原點O為極點,
為參數),以原點O為極點, ![]() 軸的非負半軸為極軸建立極坐標系,直線
軸的非負半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]()
(1)求圓C的直角坐標方程及其圓心C的直角坐標;
(2)設直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列各式中,所得數值最小的是( )
A.sin50°cos39°﹣sin40°cos51°
B.﹣2sin240°+1
C.2sin6°cos6°
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)圖象的一部分如圖所示,函數g(x)=f(x+ ![]() ),則下列結論正確的是( )
),則下列結論正確的是( ) 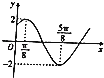
A.函數g(x)的奇函數
B.函數f(x)與g(x)的圖象均關于直線x=﹣ ![]() π對稱
π對稱
C.函數f(x)與g(x)的圖象均關于點(﹣ ![]() ,0)對稱
,0)對稱
D.函數f(x)與g(x)在區間(﹣ ![]() ,0)上均單調遞增
,0)上均單調遞增
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(sinx+ ![]() cosx)2﹣2.
cosx)2﹣2.
(1)當x∈[0, ![]() ]時,求函數f(x)的單調遞增區間;
]時,求函數f(x)的單調遞增區間;
(2)若x∈[﹣ ![]() ,
, ![]() ],求函數g(x)=
],求函數g(x)= ![]() f2(x)﹣f(x+
f2(x)﹣f(x+ ![]() )﹣1的值域.
)﹣1的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是偶函數,且f(x+ ![]() )=f(
)=f( ![]() ﹣x),當﹣
﹣x),當﹣ ![]() ≤x≤0時,f(x)=(
≤x≤0時,f(x)=( ![]() )x﹣1,記an=f(
)x﹣1,記an=f( ![]() ),n∈N+ , 則a2046的值為( )
),n∈N+ , 則a2046的值為( )
A.1﹣ ![]()
B.1﹣ ![]()
C.![]() ﹣1
﹣1![]()
D.![]() ﹣1
﹣1![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com