【題目】如圖，一智能掃地機器人在A處發現位于它正西方向的B處和北偏東
方向上的C處分別有需要清掃的垃圾，紅外線感應測量發現機器人到B的距離比到C的距離少0.4m，于是選擇沿
路線清掃.已知智能掃地機器人的直線行走速度為0.2m/s,忽略機器人吸入垃圾及在B處旋轉所用時間，10秒鐘完成了清掃任務.
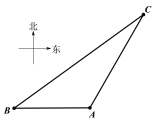
（1）B、C兩處垃圾的距離是多少？（精確到0.1）
（2）智能掃地機器人此次清掃行走路線的夾角
是多少？（用反三角函數表示）
科目：高中數學 來源： 題型：
【題目】某省在2017年啟動了“3+3”高考模式.所謂“3+3”高考模式，就是語文、數學、外語（簡稱語、數、外）為高考必考科目，從物理、化學、生物、政治、歷史、地理（簡稱理、化、生、政、史、地）六門學科中任選三門作為選考科目.該省某中學2017級高一新生共有990人，學籍號的末四位數從0001到0990.
（1）現從高一學生中抽樣調查110名學生的選考情況，問：采用什么樣的抽樣方法較為恰當?（只寫出結論，不需要說明理由）
（2）據某教育機構統計，學生所選三門學科在將來報考專業時受限制的百分比是不同的.該機構統計了受限百分比較小的十二種選擇的百分比值
，制作出如下條形圖.
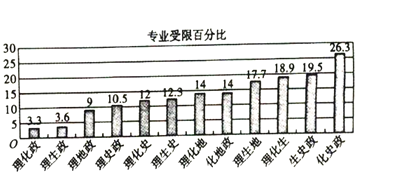
設以上條形圖中受限百分比的均值為
，標準差為
.如果一個學生所選三門學科專業受限百分比在區間
內，我們稱該選擇為“恰當選擇”.該校李明同學選擇了化學，然后從余下五門選考科目中任選兩門.問李明的選擇為“恰當選擇"的概率是多少?（均值，標準差均精確到0.1）
(參考公式和數據：
，
)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙兩人同時參加一次數學測試，共有
道選擇題，每題均有
個選項，答對得
分，答錯或不答得
分．甲和乙都解答了所有的試題，經比較，他們只有
道題的選項不同，如果甲最終的得分為
分，那么乙的所有可能的得分值組成的集合為____________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知某地區某種昆蟲產卵數和溫度有關.現收集了一只該品種昆蟲的產卵數
（個）和溫度
（
）的7組觀測數據，其散點圖如所示：
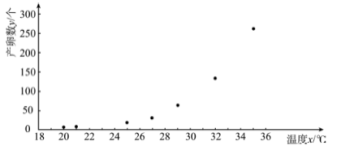
根據散點圖，結合函數知識，可以發現產卵數和溫度可用方程
來擬合，令
，結合樣本數據可知
與溫度可用線性回歸方程來擬合．根據收集到的數據，計算得到如下值：
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中
，
．
（1）求和溫度的回歸方程（回歸系數結果精確到
）；
（2）求產卵數關于溫度的回歸方程；若該地區一段時間內的氣溫在
之間（包括
與
），估計該品種一只昆蟲的產卵數的范圍.（參考數據：
，
，
，
，
．）
附：對于一組數據
，
，…，
，其回歸直線
的斜率和截距的最小二乘估計分別為
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
為數列
的前n項和, 且滿足
為常數
.
（1）若
，求
的值；
（2）是否存在實數 
，使得數列為等差數列？若存在，求出的值；若不存在，請說明理由；
（3）當
時，若數列
滿足
，且
，令
，求數列
的前n項和
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下圖是一塊平行四邊形園地
，經測量，
.擬過線段
上一點
設計一條直路
（點
在四邊形的邊上，不計直路的寬度），將該園地分為面積之比為
的左，右兩部分分別種植不同花卉.設
（單位：m）.
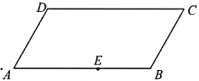
（1）當點與點
重合時，試確定點的位置；
（2）求
關于
的函數關系式；
（3）試確定點
的位置，使直路的長度最短.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，底面
為正方形，
底面，
，
為線段
的中點．
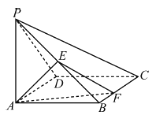
（1）若
為線段
上的動點，證明：平面
平面
；
（2）若為線段，
，
上的動點（不含
，
），
，三棱錐
的體積是否存在最大值？如果存在，求出最大值；如果不存在，請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
