等比數列{an}的各項都為正,公比q=2,且a1a2a3…a30=230,則a3a6a9…a30等于( )
A.210
B.215
C.220
D.230
【答案】
分析:由等比數列的性質,可將此數列的前三十項分為三組,每組十個數的乘積,第一組是a
1a
4a
7…a
28,第二組是a
2a
5a
8…a
29,第三組是a
3a
6a
9…a
30.此三個數是一個公比為2
10,由此關系求出答案.
解答:解:由題意可將此數列的前三十項分為三組,每組十個數的乘積,
第一組是a
1a
4a
7…a
28,第二組是a
2a
5a
8…a
29,第三組是a
3a
6a
9…a
30.此三個數是一個公比為2
10,
令t=a
3a
6a
9…a
30,則有a
1a
4a
7…a
28=

,a
2a
5a
8…a
29=

.
故有t×

×
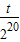
=2
30,解得t=2
20,
即a
3a
6a
9…a
30=2
20,
故選C
點評:本題考查等比數列的性質,解題的關鍵是熟練掌握數列的性質,且能根據這些性質將本題中涉及的項的乘積表示出來.代入已知的方程求值.

 ,a2a5a8…a29=
,a2a5a8…a29= .
. ×
×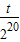 =230,解得t=220,
=230,解得t=220,
