在各項都為正數(shù)的等比數(shù)列
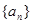
中,
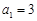
,前三項和為21,則
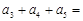
( )
分析:根據(jù)等比數(shù)列{an}中,首項a1=3,前三項和為21,可求得q,根據(jù)等比數(shù)列的通項公式,分別求得a3,a4和a5代入a3+a4+a5,即可得到答案.
解:在各項都為正數(shù)的等比數(shù)列{an}中,首項a1=3,前三項和為21
故3+3q+3q2=21,
∴q=2
∴a3+a4+a5=21×22=84
故選B
點評:本題主要考查了等比數(shù)列的性質(zhì).要理解和記憶好等比數(shù)列的通項公式,并能熟練靈活的應用.
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:單選題
若

是方程
 2
2-

m

+m=0的兩實根,且

、

、

成等比數(shù)列,則實數(shù)m的值為
A. | B.0或 | C.0 | D.2 |
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
已知等比數(shù)列

的前三項依次為
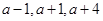
,則數(shù)列的通項公式
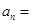
( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
等比數(shù)列{a
n}中,a
2=9,a
5=243,則{a
n}的前4項和為( ).
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
記等差數(shù)列
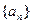
的前
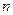
項的和為
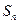
, 利用倒序求和的方法得:
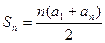
;類似地,記等比數(shù)列
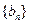
的前
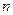
項的積為
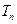
,且
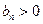
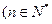
),試類比等差數(shù)列求和的方法,可將
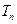
表示成首項
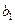
,末項
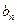
與項數(shù)
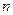
的一個關(guān)系式,即
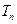
=_____________.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
(本小題滿分12分)等比數(shù)列{a
n}的各項均為正數(shù),且2a
1+3a
2=1,a=9a
2a
6.
(1)求數(shù)列{a
n}的通項公式;
(2)設(shè)b
n=log
3a
1+log
3a
2+…+log
3a
n,求數(shù)列

的前n項和.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
在等比數(shù)列
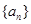
中,
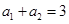
,
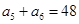
,則
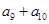
等于( )
| A. 16 | B. 256 | C. 768 | D.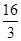 |
查看答案和解析>>

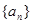 中,
中,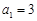 ,前三項和為21,則
,前三項和為21,則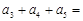 ( )
( ) 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案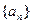 的前
的前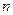 項的和為
項的和為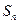 , 利用倒序求和的方法得:
, 利用倒序求和的方法得: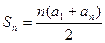 ;類似地,記等比數(shù)列
;類似地,記等比數(shù)列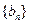 的前
的前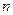 項的積為
項的積為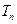 ,且
,且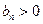
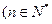 ),試類比等差數(shù)列求和的方法,可將
),試類比等差數(shù)列求和的方法,可將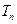 表示成首項
表示成首項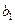 ,末項
,末項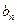 與項數(shù)
與項數(shù)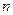 的一個關(guān)系式,即
的一個關(guān)系式,即 =_____________.
=_____________. 的前n項和.
的前n項和.