
 ,知當且僅當a=b時,a+b最小,即農田面積最小,
,知當且僅當a=b時,a+b最小,即農田面積最小,

 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數學 來源: 題型:解答題
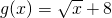 時,甲、乙兩公司為了避免惡性競爭,經過協商,同意在雙方均無失敗風險的情況下盡可能的少投入宣傳費用,問此時甲乙兩公司應各投入多少宣傳費用?
時,甲、乙兩公司為了避免惡性競爭,經過協商,同意在雙方均無失敗風險的情況下盡可能的少投入宣傳費用,問此時甲乙兩公司應各投入多少宣傳費用?查看答案和解析>>
科目:高中數學 來源: 題型:解答題
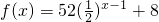 ,乙工人所用的時間為
,乙工人所用的時間為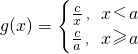 (a,c為常數)(單位:分鐘).已知乙工人組裝第4件產品用時15分鐘,組裝第a件產品用時10分鐘.
(a,c為常數)(單位:分鐘).已知乙工人組裝第4件產品用時15分鐘,組裝第a件產品用時10分鐘.查看答案和解析>>
科目:高中數學 來源: 題型:單選題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com