
【題目】已知函數![]() ,其中
,其中![]() .
.
(1)當![]() 時,求證:
時,求證:![]() 時,
時,![]() ;
;
(2)試討論函數![]() 的零點個數.
的零點個數.
【答案】(1)見解析;(2)當![]() 時,有兩個零點;當
時,有兩個零點;當![]() 時;有且僅有一個零點.
時;有且僅有一個零點.
【解析】
試題分析:(1)首先將![]() 代入函數解析式,然后令
代入函數解析式,然后令![]() ,再通過求導得到
,再通過求導得到![]() 的單調性,從而使問題得證;(2)首先求得
的單調性,從而使問題得證;(2)首先求得![]() ,然后求得
,然后求得![]() 時
時![]() 的值,再對
的值,再對![]() 分類討論,通過構造函數,利用導數研究函數單調性極值與最值,即可得出函數零點的個數.
分類討論,通過構造函數,利用導數研究函數單調性極值與最值,即可得出函數零點的個數.
試題解析:(1)當![]() 時,令
時,令![]() (
(![]() ),則
),則![]() ,
,
當![]() 時,
時,![]() ,
,![]() ,
,![]()
![]() ,此時函數
,此時函數![]() 遞增,
遞增,
![]() 當
當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ………①
………①
(2) ………②,令
………②,令![]() ,得
,得![]() ,
,![]() ,
,
(i)當![]() 時,
時,![]() ,由②得
,由②得![]() ……③
……③
![]() 當
當![]() 時,
時,![]() ,
,![]() ,
,![]()
![]() ,此時,函數
,此時,函數![]() 為增函數,
為增函數,
![]()
![]() 時,
時,![]() ,
,![]() ,
,![]() 時,
時,![]() ,
,
故函數![]() ,在
,在![]() 上有且只有一個零點
上有且只有一個零點![]() ;
;
(ii)當![]() 時,
時,![]() ,且
,且![]() ,
,
由②知,當![]() ,
,![]() ,
,![]() ,
,![]() ,
,
此時,![]() ;同理可得,當
;同理可得,當![]() ,
,![]() ;當
;當![]() 時,
時,![]() ;
;
![]() 函數
函數![]() 的增區間為
的增區間為![]() 和
和![]() ,減區間為
,減區間為![]()
故,當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]()
![]() 函數
函數![]() ,
,![]() 有且只有一個零點
有且只有一個零點![]() ;
;
又![]() ,構造函數
,構造函數![]() ,
,![]() ,則
,則
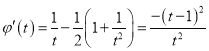 ……④,易知,對
……④,易知,對![]() ,
,![]() ,
,![]() 函數
函數![]() ,
,
![]() 為減函數,
為減函數,![]()
![]()
由![]() ,知
,知![]() ,
,![]()
![]() ……⑤
……⑤
構造函數![]() (
(![]() ),則
),則![]() ,當
,當![]() 時,
時,![]() ,當
,當![]()
時,![]() ,
,![]() 函數
函數![]() 的增區間為
的增區間為![]() ,減區間為
,減區間為![]() ,
,![]()
![]() ,
,
![]() 有
有![]() ,則
,則![]() ,
,
![]()
 ,當
,當 時,
時,![]() ……⑥
……⑥
而![]() ……⑦
……⑦
由⑥⑦知![]() ……⑧
……⑧
又函數![]() 在
在![]() 上遞增,
上遞增,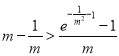
由⑤⑧和函數零點定理知,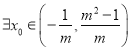 ,使得
,使得![]()
綜上,當![]() 時,函數
時,函數![]() 有兩個零點,
有兩個零點,
綜上所述:當![]() 時,函數
時,函數![]() 有兩個零點,
有兩個零點,
當![]() 時,函數
時,函數![]() 有且僅有一個零點.
有且僅有一個零點.


科目:高中數學 來源: 題型:
【題目】如圖所示的幾何體中,四邊形ABCD是矩形,平面ABCD⊥平面ABE,已知AB=2,AE=BE=![]() ,且當規定主視圖方向垂直平面ABCD時,該幾何體的側視圖的面積為
,且當規定主視圖方向垂直平面ABCD時,該幾何體的側視圖的面積為![]() .若M、N分別是線段DE、CE上的動點,則AM+MN+NB的最小值為________.
.若M、N分別是線段DE、CE上的動點,則AM+MN+NB的最小值為________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中正確的為( )
A. 線性相關系數r越大,兩個變量的線性相關性越強
B. 線性相關系數r越小,兩個變量的線性相關性越弱
C. 用相關指數R2來刻畫回歸效果,R2越小,說明模型的擬合效果越好
D. 殘差平方和越小的模型,模型擬合的效果越好
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 及點
及點![]() .
.
(Ⅰ)若線段![]() 的垂直平分線交圓
的垂直平分線交圓![]() 于
于![]() 兩點,試判斷四邊形
兩點,試判斷四邊形![]() 的形狀,并給與證明;
的形狀,并給與證明;
(Ⅱ)過點![]() 的直線
的直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,當
兩點,當![]() 的面積最大時,求直線
的面積最大時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() (
(![]() )的左右焦點分別為
)的左右焦點分別為![]() ,
,![]() ,且離心率為
,且離心率為![]() ,點
,點![]() 為橢圓上一動點,
為橢圓上一動點,![]() 面積的最大值為
面積的最大值為![]() .
.
(1)求橢圓的方程;
(2)設橢圓的左頂點為![]() ,過右焦點
,過右焦點![]() 的直線
的直線![]() 與橢圓相交于
與橢圓相交于![]() ,
,![]() 兩點,連結
兩點,連結![]() ,
,![]() 并延長交直線
并延長交直線![]() 分別于
分別于![]() ,
,![]() 兩點,問
兩點,問![]() 是否為定值?若是,求出此定值;若不是,請說明理由.
是否為定值?若是,求出此定值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,其中
,其中![]() .
.
(1)當![]() 時,求曲線
時,求曲線 ![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)求函數的單調區間與極值;
(3)已知函數![]() 有三個互不相同的零點
有三個互不相同的零點![]() ,且
,且![]() .若對
.若對![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)的定義域為(0,+∞),且在(0, +∞)是遞增的,![]()
(1)求證:f(1)=0,f(xy)=f(x)+ f(x)
(2)設f(2)=1,解不等式![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下面兩個程序最后輸出的S的值為( )
程序1:
i=1;
while i<8
i=i+2;
S=2i+3;
end
print(%io(2),S);
程序2:
i=1;
while i<8
S=2i+3;
i=i+2;
end
print(%io(2),S);
A. 都是17 B. 都是21
C. 21,17 D. 17,21
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com