【題目】電視傳媒公司為了解某地區觀眾對某類休育節目的收視情況，隨機抽取了100名觀眾進行調查，其中女性有55名.下面是根據調查結果繪制的觀眾日均收看該體育節目時間的頻率分布直方圖：
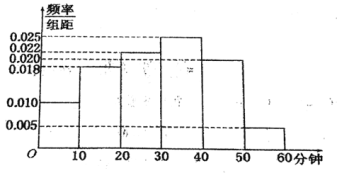
將日均收看該體育節目時間不低于40分鐘的觀眾稱為“體育迷”，已知“體育迷”中有10名女性.
（1）根據已知條件完成下面的
列聯表，并據此資料判斷是否有
的把握認為“體育迷”與性別有關？
非體育迷 | 體育迷 | 合計 | |
男 | |||
女 | |||
合計 |
（2）將日均收看讀體育節目不低于50分鐘的觀眾稱為“超級體育迷”，已知“超級體育迷”中有2名女性，若從“超級體育迷”中任意選取2人，求至少有1名女性觀眾的概率.
附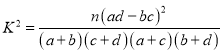
.
| 0.05 | 0.01 |
| 3.841 | 6.635 |
【答案】（1）填表見解析；沒有
的把握認為“體育迷”與性別有關（2）
【解析】
（1）根據頻率分布直方圖，在抽取的100人中，其中女性有55名，“體育迷”有25人，其中有10名女性完成
列聯表，.然后計算
值，與
表對照下結論.
（2）由頻率分布直方圖可知，“超級體育迷”為5人，其中3名男性，2名女性，根據古典概型，先列舉一切可能結果所組成的基本事件數，再找出“任選2人中，至少有1人是女性”的基本事件數，代入公式求解.
（1）由頻率分布直方圖可知，在抽取的100人中，“體育迷”有25人，從而完成列聯表如下：
非體育迷 | 體育迷 | 合計 | |
男 | 30 | 15 | 45 |
女 | 45 | 10 | 55 |
合計 | 75 | 25 | 100 |
將列聯表中的數據代入公式計算，得
.
因為
，
所以我們沒有的把握認為“體育迷”與性別有關.
（2）由頻率分布直方圖可知，“超級體育迷”為5人，其中
表示男性，
，
表示女性，
，
從而一切可能結果所組成的基本事件為
，
，
，
，
，
，
，
，
，
， 由10個基本事件組成，而且這些基本事件的出現是等可能的.
用
表示“任選2人中，至少有1人是女性”這一事件，則，，，，，，，由7個基本事件組成，
所以
.
假期作業暑假成長樂園新疆青少年出版社系列答案科目：高中數學 來源： 題型：
【題目】已知集合A＝{x|2a＋1≤x≤3a－5}，B＝{x|x＜－1，或x＞16}，分別根據下列條件求實數a的取值范圍．
（1）A∩B＝
；（2）A（A∩B）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖1，有一邊長為2的正方形ABCD，E是邊AD的中點，將
沿著直線BE折起至
位置（如圖2），此時恰好
，點
在底面上的射影為O.
（1）求證：
；
（2）求直線
與平面BCDE所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】用清水漂洗衣服上殘留的洗衣液，對用一定量的清水漂洗一次的效果作如下假定：用1個單位量的水可洗掉衣服上殘留洗衣液質量的一般，用水越多漂洗效果越好，但總還有洗衣液殘留在衣服上.設用
單位量的清水漂洗一次后，衣服上殘留的洗衣液質量與本次漂洗前殘留的洗衣液質量之比為函數
，其中
.
（1）試規定
的值，并解釋其實際意義；
（2）根據假定寫出函數應該滿足的條件和具有的性質，并寫出滿足假定的一個指數函數；
（3）設函數
.現有
（
）單位量的清水，可供漂洗一次，也可以把水平均分成2份后先后漂洗兩次，試確定哪種方式漂洗效果更好？并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
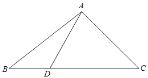
【題目】如圖所示，在△ABC中，D是BC邊上的一點，且AB=14，BD=6，∠ADC=
，
．
（Ⅰ）求sin∠DAC；
（Ⅱ）求AD的長和△ABC的面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
年
月
日是第二十七屆“世界水日”，月
日是第三十二屆“中國水周”．我國紀念年“世界水日”和“中國水周”活動的宣傳主題為“堅持節水優先，強化水資源管理”．某中學課題小組抽取
、
兩個小區各
戶家庭，記錄他們
月份的用水量（單位：
）如下表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
（1）根據兩組數據完成下面的莖葉圖，從莖葉圖看，哪個小區居民節水意識更好？
|
| |
| ||
| ||
| ||
|
（2）從用水量不少于
的家庭中，、兩個小區各隨機抽取一戶，求小區家庭的用水量低于小區的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
