【題目】四棱錐
中，側(cè)面
是邊長為
的正三角形，且與底面垂直，底面
是
的菱形， 
為
的中點， 
為
的中點.
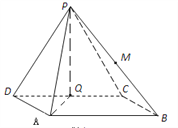
（1）求證： 
；
（2）求
與平面
所成的角.
時刻準備著暑假作業(yè)原子能出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案
假期作業(yè)暑假成長樂園新疆青少年出版社系列答案科目：高中數(shù)學 來源： 題型：
【題目】已知函數(shù)
（
為常數(shù)），函數(shù)
，（
為常數(shù)，且
）.
（1）若函數(shù)
有且只有1個零點，求的取值的集合.
（2）當（1）中的取最大值時，求證：
.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知橢圓
： 
過點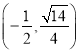
，且離心率為
.過點
的直線
與橢圓
交于
， 
兩點.
（Ⅰ）求橢圓
的標準方程；
（Ⅱ）若點
為橢圓
的右頂點，探究： 
是否為定值，若是，求出該定值，若不是，請說明理由.（其中， 
， 
分別是直線
、
的斜率）
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】如圖，三棱柱
中，側(cè)棱
底面
，且各棱長均相等， 
分別為棱
的中點.
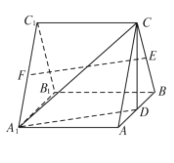
（1）證明
平面
；
（2）證明平面
平面
；
（3）求直線
與平面
所成角的正弦值.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】設函數(shù)
的反函數(shù)為
，若存在函數(shù)
使得對函數(shù)定義域內(nèi)的任意
都有
，則稱函數(shù)為函數(shù)的“Inverse”函數(shù).
（1）判斷下列哪個函數(shù)是函數(shù)
的“Inverse”函數(shù)并說明理由.
①
；②
；
（2）設函數(shù)存在反函數(shù)，證明函數(shù)存在唯一的“Inverse”函數(shù)的充要條件是函數(shù)的值域為
；
（3）設函數(shù)
存在反函數(shù)，函數(shù)為的一個“Inverse”函數(shù)，記
，其中
，若對函數(shù)定義域內(nèi)的任意都有
，求所有滿足條件的函數(shù)的解析式.
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】已知
是定義域為
上的函數(shù)，若對任意的實數(shù)
，都有：
成立，當且僅當
時取等號，則稱函數(shù)是上的凸函數(shù)，凸函數(shù)具有以下性質(zhì)：對任意的實數(shù)
，都有：
成立，當且僅當
時取等號，設
（1）求證：
是
上的凸函數(shù)
（2）設
，
，利用凸函數(shù)的定義求
的最大值
（3）設
是
三個內(nèi)角，利用凸函數(shù)性質(zhì)證明
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】某電視臺為宣傳本省，隨機對本省內(nèi)
歲的人群抽取了n人，回答問題“本省內(nèi)著名旅游景點有哪些”統(tǒng)計結(jié)果如圖表所示
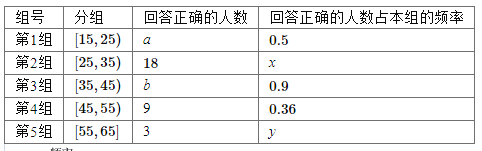
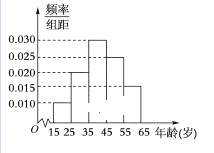
（1）分別求出
的值；
（2）從第
組回答正確的人中用分層抽樣的方法抽取6人，求第組每組各抽取多少人？
（3）指出直方圖中，這組數(shù)據(jù)的中位數(shù)是多少（取整數(shù)值）？
查看答案和解析>>
科目：高中數(shù)學 來源： 題型：
【題目】（12分）已知函數(shù)f（x）=
（1）判斷函數(shù)在區(qū)間[1,+∞）上的單調(diào)性,并用定義證明你的結(jié)論．
（2）求該函數(shù)在區(qū)間[1,4]上的最大值與最小值．
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
