
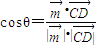 可以求解
可以求解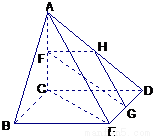 (1)證明:由圖(甲)結合已知條件知四邊形CBED為正方形
(1)證明:由圖(甲)結合已知條件知四邊形CBED為正方形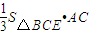
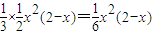 =
=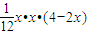 --------------(7分)
--------------(7分)
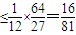
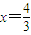 時取“=”
時取“=”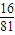 -------------------------------------------(9分)
-------------------------------------------(9分)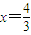 ,即BC=
,即BC=
 ,∴B
,∴B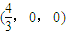 ,
,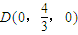 ,
,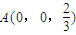 -----(10分)
-----(10分)
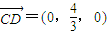
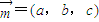
 ,
,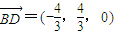 -------------(11分)
-------------(11分)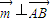 ,
, 得
得 ,
,
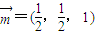 ----------------------------------------(12分)
----------------------------------------(12分)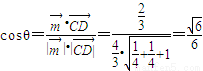 ---(14分)
---(14分)

科目:高中數學 來源: 題型:
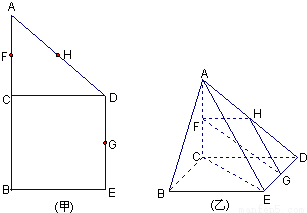
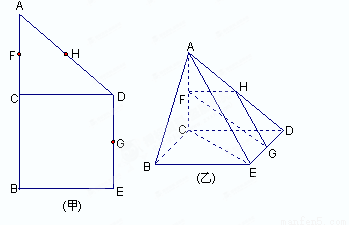
 如圖(甲),在直角梯形ABED中,AB∥DE,AB⊥BE,AB⊥CD,且BC=CD,AB=2,F、H、G分別為AC,AD,DE的中點,現將△ACD沿CD折起,使平面ACD⊥平面CBED,如圖(乙).
如圖(甲),在直角梯形ABED中,AB∥DE,AB⊥BE,AB⊥CD,且BC=CD,AB=2,F、H、G分別為AC,AD,DE的中點,現將△ACD沿CD折起,使平面ACD⊥平面CBED,如圖(乙).查看答案和解析>>
科目:高中數學 來源: 題型:

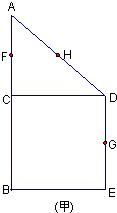 如圖(甲),在直角梯形ABED中,AB∥DE,AB⊥BE,AB⊥CD,且BC=CD,AB=2,F、H、G分別為AC,AD,DE的中點,現將△ACD沿CD折起,使平面ACD⊥平面CBED,如圖(乙).
如圖(甲),在直角梯形ABED中,AB∥DE,AB⊥BE,AB⊥CD,且BC=CD,AB=2,F、H、G分別為AC,AD,DE的中點,現將△ACD沿CD折起,使平面ACD⊥平面CBED,如圖(乙).查看答案和解析>>
科目:高中數學 來源:2013屆江西省高三10月月考理科數學試卷(解析版) 題型:解答題
(本小題滿分13分)如圖(甲),在直角梯形ABED中,AB//DE,AB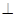 BE,AB
BE,AB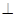 CD,且BC=CD,AB=2,F、H、G分別為AC ,AD ,DE的中點,現將△ACD沿CD折起,使平面ACD
CD,且BC=CD,AB=2,F、H、G分別為AC ,AD ,DE的中點,現將△ACD沿CD折起,使平面ACD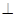 平面CBED,如圖(乙).
平面CBED,如圖(乙).
(1)求證:平面FHG//平面ABE;
(2)記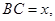
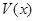 表示三棱錐B-ACE
的體積,求
表示三棱錐B-ACE
的體積,求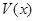 的最大值;
的最大值;
(3)當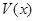 取得最大值時,求二面角D-AB-C的余弦值.
取得最大值時,求二面角D-AB-C的余弦值.
查看答案和解析>>
科目:高中數學 來源:2012-2013學年江西省高三第二次(10月)月考理科數學試卷(解析版) 題型:解答題
(本小題滿分13分)如圖(甲),在直角梯形ABED中,AB//DE,AB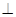 BE,AB
BE,AB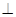 CD,且BC=CD,AB=2,F、H、G分別為AC ,AD ,DE的中點,現將△ACD沿CD折起,使平面ACD
CD,且BC=CD,AB=2,F、H、G分別為AC ,AD ,DE的中點,現將△ACD沿CD折起,使平面ACD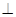 平面CBED,如圖(乙).
平面CBED,如圖(乙).
(1)求證:平面FHG//平面ABE;
(2)記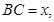
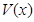 表示三棱錐B-ACE
的體積,求
表示三棱錐B-ACE
的體積,求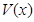 的最大值;
的最大值;
(3)當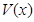 取得最大值時,求二面角D-AB-C的余弦值.
取得最大值時,求二面角D-AB-C的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com