
【題目】閱讀下面一道題目的證明,指出其中的一處錯誤。題目:平面上有六個點,任何三點都是三邊互不相等三角形的頂點,則這些三角形中有一個的最短邊又是另一個三角形的最長邊。證明:第一步,對已知的六個點作兩兩連線,可以得出15條邊,記為![]() ,
,![]() ,…,
,…,![]() .第二步,由于任何三點組成的都是“三邊互不相等的三角形”,因此,15條邊互不相等不妨設
.第二步,由于任何三點組成的都是“三邊互不相等的三角形”,因此,15條邊互不相等不妨設![]() .第三步,由于“任何三點都是三邊互不相等三角形的頂點”,因此,任取三條邊都可以組成三角形,則
.第三步,由于“任何三點都是三邊互不相等三角形的頂點”,因此,任取三條邊都可以組成三角形,則![]() 、
、![]() 、
、![]() 組成的三角形的最長邊
組成的三角形的最長邊![]() ,也是
,也是![]() 、
、![]() 、
、![]() 組成的三角形的最短邊,命題得證.這三步中,第______步有錯誤,理由是______.
組成的三角形的最短邊,命題得證.這三步中,第______步有錯誤,理由是______.
【答案】二或三 第三步有錯誤,理由是:不能推出“任取三條邊都可以組成三角形”或第二步有錯誤,理由是:不能推出![]() .
.
【解析】
不能推出“任取三條邊都可以組成三角形”,
比如,從六個點![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中,記
中,記![]() 、
、![]() 的連線為
的連線為![]() ,記
,記![]() 、
、![]() 的連線為
的連線為![]() ,記
,記![]() 、
、![]() 的連線為
的連線為![]() (
(![]() 、
、![]() 、
、![]() 互不相等),
互不相等),
則![]() 、
、![]() 、
、![]() 未必能組成三角形,即使組成三角形也不是本題所說的“三點兩兩連線”所成的三角形。
未必能組成三角形,即使組成三角形也不是本題所說的“三點兩兩連線”所成的三角形。
第二步也有錯誤,理由是三點組成的“單個三角形”內部邊長互不相等,
不能推出“多個三角形”之間邊長互不相等,因而,“![]() ”中的“
”中的“![]() ”也可能有“
”也可能有“![]() ”。
”。
說明:雖然證明有錯誤,但結論是成立的,可把六個點“兩兩連線”的每個三角形最長邊染成紅色,剩下的邊染成藍色,然后證明必有同色三角形,
又因為每個三角形都有紅邊,所以,同色三角形必有三邊同紅色的三角形,這個三角形的最短邊便又是另一個三角形的最長邊。


 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:高中數學 來源: 題型:
【題目】為調研高中生的作文水平.在某市普通高中的某次聯考中,參考的文科生與理科生人數之比為![]() ,且成績分布在
,且成績分布在![]() 的范圍內,規定分數在50以上(含50)的作文被評為“優秀作文”,按文理科用分層抽樣的方法抽取400人的成績作為樣本,得到成績的頻率分布直方圖,如圖所示.其中
的范圍內,規定分數在50以上(含50)的作文被評為“優秀作文”,按文理科用分層抽樣的方法抽取400人的成績作為樣本,得到成績的頻率分布直方圖,如圖所示.其中![]() 構成以2為公比的等比數列.
構成以2為公比的等比數列.
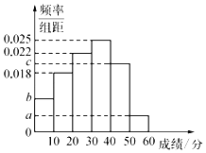
(1)求![]() 的值;
的值;
(2)填寫下面![]() 列聯表,能否在犯錯誤的概率不超過0.01的情況下認為“獲得優秀作文”與“學生的文理科”有關?
列聯表,能否在犯錯誤的概率不超過0.01的情況下認為“獲得優秀作文”與“學生的文理科”有關?
文科生 | 理科生 | 合計 | |
獲獎 | 6 | ||
不獲獎 | |||
合計 | 400 |
(3)將上述調查所得的頻率視為概率,現從全市參考學生中,任意抽取2名學生,記“獲得優秀作文”的學生人數為![]() ,求
,求![]() 的分布列及數學期望.
的分布列及數學期望.
附: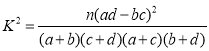 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (其中
(其中![]() 是自然對數的底數).
是自然對數的底數).
(1)證明:①當![]() 時,
時,![]() ;
;
②當![]() 時,
時,![]() .
.
(2)是否存在最大的整數![]() ,使得函數
,使得函數![]() 在其定義域上是增函數?若存在,求
在其定義域上是增函數?若存在,求![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】成等差數列的三個正數的和等于15,并且這三個數分別加上2、5、13后成為等比數列{bn}中的b3、b4、b5.
(Ⅰ)求數列{bn}的通項公式;
(Ⅱ)數列{bn}的前n項和為Sn,求證:數列{Sn+![]() }是等比數列.
}是等比數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】黨的十九大明確把精準脫貧作為決勝全面建成小康社會必須打好的三大攻堅戰之一. 堅決打贏脫貧攻堅戰,某幫扶單位為幫助定點扶貧村真脫貧,堅持扶貧同扶智相結合,幫助貧困村中60戶農民種植蘋果、40戶農民種植梨、20戶農民種植草莓(每戶僅扶持種植一種水果),為了更好地了解三種水果的種植與銷售情況,現從該村隨機選6戶農民作為重點考察對象;
(1)用分層抽樣的方法,應選取種植蘋果多少戶?
(2)在上述抽取的6戶考察對象中隨機選2戶,求這2戶種植水果恰好相同的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為等差數列,
為等差數列,![]() 為等比數列,公比為q(q≠1).令A=
為等比數列,公比為q(q≠1).令A=![]() .A={1,2},
.A={1,2},
(1)當![]() ,求數列
,求數列![]() 的通項公式;
的通項公式;
(2)設![]() ,q>0,試比較
,q>0,試比較![]() 與
與![]() (n≥3)的大小?并證明你的結論.
(n≥3)的大小?并證明你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com