
【題目】已知動點P到點![]() 的距離與它到直線l:
的距離與它到直線l:![]() 的距離d的比值為
的距離d的比值為![]() ,設動點P形成的軌跡為曲線C.
,設動點P形成的軌跡為曲線C.
(Ⅰ)求曲線C的方程;
(Ⅱ)過點![]() 的直線與曲線C交于A,B兩點,設
的直線與曲線C交于A,B兩點,設![]() ,
,![]() ,過A點作
,過A點作![]() ,垂足為
,垂足為![]() ,過B點作
,過B點作![]() ,垂足為
,垂足為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
 英才點津系列答案
英才點津系列答案 紅果子三級測試卷系列答案
紅果子三級測試卷系列答案 課堂練加測系列答案
課堂練加測系列答案科目:高中數學 來源: 題型:
【題目】已知雙曲線![]() :
:![]() 的焦距為
的焦距為![]() ,直線
,直線![]() (
(![]() )與
)與![]() 交于兩個不同的點
交于兩個不同的點![]() 、
、![]() ,且
,且![]() 時直線
時直線![]() 與
與![]() 的兩條漸近線所圍成的三角形恰為等邊三角形.
的兩條漸近線所圍成的三角形恰為等邊三角形.
(1)求雙曲線![]() 的方程;
的方程;
(2)若坐標原點![]() 在以線段
在以線段![]() 為直徑的圓的內部,求實數
為直徑的圓的內部,求實數![]() 的取值范圍;
的取值范圍;
(3)設![]() 、
、![]() 分別是
分別是![]() 的左、右兩頂點,線段
的左、右兩頂點,線段![]() 的垂直平分線交直線
的垂直平分線交直線![]() 于點
于點![]() ,交直線
,交直線![]() 于點
于點![]() ,求證:線段
,求證:線段![]() 在
在![]() 軸上的射影長為定值.
軸上的射影長為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定整數![]() (
(![]() ),設集合
),設集合![]() ,記集合
,記集合![]() .
.
(1)若![]() ,求集合
,求集合![]() ;
;
(2)若![]() 構成以
構成以![]() 為首項,
為首項,![]() (
(![]() )為公差的等差數列,求證:集合
)為公差的等差數列,求證:集合![]() 中的元素個數為
中的元素個數為![]() ;
;
(3)若![]() 構成以
構成以![]() 為首項,
為首項,![]() 為公比的等比數列,求集合
為公比的等比數列,求集合![]() 中元素的個數及所有元素之和.
中元素的個數及所有元素之和.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() 為橢圓E:
為橢圓E:![]() 的左、右焦點,過點
的左、右焦點,過點![]() 的直線l與橢圓E有且只有一個交點T.
的直線l與橢圓E有且只有一個交點T.
(1)求![]() 面積的取值范圍.
面積的取值范圍.
(2)若有一束光線從點![]() 射出,射在直線l上的T點上,經過直線l反射后,試問反射光線是否恒過定點?若是,請求出該定點;若否,請說明理由.
射出,射在直線l上的T點上,經過直線l反射后,試問反射光線是否恒過定點?若是,請求出該定點;若否,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國歷法中將一年分為春、夏、秋、冬四個季節,每個季節有六個節氣,如夏季包含立夏、小滿、芒種、夏至、小暑以及大暑.某美術學院甲、乙、丙、丁四位同學接到繪制二十四節氣的彩繪任務,現四位同學抽簽確定各自完成哪個季節中的六幅彩繪,在制簽及抽簽公平的前提下,甲沒有抽到繪制春季六幅彩繪任務且乙沒有抽到繪制夏季六幅彩繪任務的概率為_________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】人耳的聽力情況可以用電子測聽器檢測,正常人聽力的等級為![]() (分貝),并規定測試值在區間
(分貝),并規定測試值在區間![]() 為非常優秀,測試值在區間
為非常優秀,測試值在區間![]() 為優秀,某班
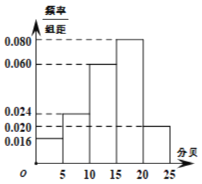
為優秀,某班![]() 名同學都進行了聽力測試,所得測試值制成頻率分布直方圖:
名同學都進行了聽力測試,所得測試值制成頻率分布直方圖:
(Ⅰ)現從聽力等級為![]() 的同學中任意抽取出4人,記聽力非常優秀的同學人數為
的同學中任意抽取出4人,記聽力非常優秀的同學人數為![]() ,求
,求![]() 的分布列與數學期望:
的分布列與數學期望:
(Ⅱ)現選出一名同學參加另一項測試,測試規則如下:四個音叉的發生情況不同,由強到弱的次序分別為1,2,3,4.測試前將音叉隨機排列,被測試的同學依次聽完后給四個音叉按發音的強弱標出一組序號![]() (其中
(其中![]() 為1,2,3,4的一個排列),記
為1,2,3,4的一個排列),記![]() ,可用
,可用![]() 描述兩次排序的偏離程度,求
描述兩次排序的偏離程度,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據有關資料預測,某市下月1—14日的空氣質量指數趨勢如下圖所示.,根據已知折線圖,解答下面的問題:
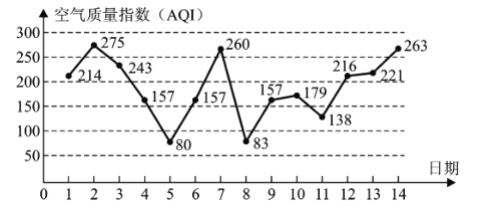
(1)求污染指數的眾數及前五天污染指數的平均值;(保留整數)
(2)為了更好發揮空氣質量監測服務人民的目的,監測部門在發布空氣質量指數的同時,也給出了出行建議,比如空氣污染指數大于150時需要戴口罩,超過200時建議減少外出活動等等.如果某人事先沒有注意到空氣質量預報,而在1—12號這12天中隨機選定一天,欲在接下來的兩天中(不含選定當天)進行外出活動.求其外出活動的兩天期間.
①恰好都遭遇重度及以上污染天氣的概率;
②至少有一天能避開重度及以上污染天氣的概率.
附:空氣質量等級參考表:
|
|
|
|
|
|
|
等級 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com