
【題目】已知函數(shù)![]() ,
, ![]() ,其中
,其中![]() .
.
(1)當![]() 時,求函數(shù)
時,求函數(shù)![]() 的值域;
的值域;
(2)若對任意![]() ,均有
,均有![]() ,求
,求![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,設
時,設 ,若
,若![]() 的最小值為
的最小值為![]() ,求實數(shù)
,求實數(shù)![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() .
.
【解析】試題分析:(1)當a=0時, ![]() ,,借助換元法及二次函數(shù)圖象及性質即可求函數(shù)g(x)的值域;
,,借助換元法及二次函數(shù)圖象及性質即可求函數(shù)g(x)的值域;
(2)分類討論,|f(x)|≤2,可化為![]() ,變量分離,構建新函數(shù)求最值,即可求a的取值范圍;
,變量分離,構建新函數(shù)求最值,即可求a的取值范圍;
(3)分類討論,利用配方法,結合![]() 的最小值為
的最小值為![]() ,求實數(shù)a的值.
,求實數(shù)a的值.
試題解析:
(1)當![]() 時,
時, ![]() ,
,
因為![]() ,
,
所以![]() ,
, ![]() 的值域為
的值域為![]()
(2)若![]() ,
, ![]()
若![]() 時,
時, ![]() 可化為
可化為![]()
即![]() ,所以
,所以![]()
因為![]() 在
在![]() 為遞增函數(shù),所以函數(shù)
為遞增函數(shù),所以函數(shù)![]() 的最大值為
的最大值為![]() ,
,
因為![]() (當且僅當
(當且僅當![]() ,即
,即![]() 取“
取“![]() ”)
”)
所以![]() 的取值范圍是
的取值范圍是![]() .
.
(3)因為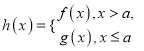 當
當![]() 時,
時, ![]() ,
,
令![]() ,
, ![]() ,則
,則![]()
![]() ,
,
當![]() 時,即
時,即![]() ,
, ![]() ;
;
當![]() 時,
時, ![]() ,即
,即![]() ,
,
因為![]() ,所以
,所以![]() ,
, 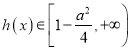 .
.
若![]() ,
, ![]() ,此時
,此時![]() ,
,
若![]() ,即
,即![]() ,此時
,此時![]() ,所以實數(shù)
,所以實數(shù)![]() .
.


 期末寶典單元檢測分類復習卷系列答案
期末寶典單元檢測分類復習卷系列答案科目:高中數(shù)學 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c,S表示△ABC的面積,若acosB+bcosA=csinC,S= ![]() (b2+c2﹣a2),則∠B=( )
(b2+c2﹣a2),則∠B=( )
A.90°
B.60°
C.45°
D.30°
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,直角三角形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 為線段
為線段![]() 上一點,且
上一點,且![]() ,沿
,沿![]() 邊上的中線
邊上的中線![]() 將
將![]() 折起到
折起到![]() 的位置.
的位置.
(Ⅰ)求證: ![]() ;
;
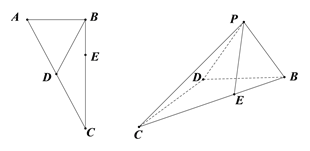
(Ⅱ)當平面![]() 平面
平面![]() 時,求二面角
時,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知數(shù)列![]() 和
和![]() 滿足
滿足![]() 若
若![]() 為等比數(shù)列,且
為等比數(shù)列,且![]()
(1)求![]() 和
和![]() ;
;
(2)設![]() ,記數(shù)列
,記數(shù)列![]() 的前
的前![]() 項和為
項和為![]()
①求![]() ;
;
②求正整數(shù) k,使得對任意![]() 均有
均有![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,
, ![]() ,
, ![]() ,
, ![]()
(1)求證:函數(shù)![]() 在點
在點![]() 處的切線恒過定點,并求出定點的坐標;
處的切線恒過定點,并求出定點的坐標;
(2)若![]() 在區(qū)間
在區(qū)間![]() 上恒成立,求
上恒成立,求![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,求證:在區(qū)間
時,求證:在區(qū)間![]() 上,滿足
上,滿足![]() 恒成立的函數(shù)
恒成立的函數(shù)![]() 有無窮多個.(記
有無窮多個.(記![]() )
)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知f(x)為定義在[﹣1,1]上的奇函數(shù),當x∈[﹣1,0]時,函數(shù)解析式為 ![]() .
.
(Ⅰ)求f(x)在[0,1]上的解析式;
(Ⅱ)求f(x)在[0,1]上的最值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設f(x)是定義在R上的函數(shù),對任意實數(shù)m,n,都有f(m)f(n)=f(m+n),且當x<0時,0<f(x)<1.
(1)證明:①f(0)=1;②當x>0時,f(x)>1;③f(x)是R上的增函數(shù);
(2)設a∈R,試解關于x的不等式f(x2﹣3ax+1)f(﹣3x+6a+1)≤1.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】下列四組函數(shù)中表示同一個函數(shù)的是( )
A.f(x)=|x|與 ![]()
B.f(x)=x0與g(x)=1
C.![]() 與
與 ![]()
D.![]() 與
與 ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設函數(shù)f(x)=2cos2x+ ![]() sin2x﹣1.
sin2x﹣1.
(1)求f(x)的最大值及此時的x值
(2)求f(x)的單調減區(qū)間
(3)若x∈[﹣ ![]() ,
, ![]() ]時,求f(x)的值域.
]時,求f(x)的值域.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com