
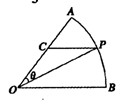
如圖所示,扇形AOB,圓心角AOB的大小等于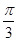 ,半徑為2,在半徑OA上有一動點C,過點C作平行于OB的直線交弧AB于點P.
,半徑為2,在半徑OA上有一動點C,過點C作平行于OB的直線交弧AB于點P.
(1)若C是半徑OA的中點,求線段PC的長;
(2)設(shè)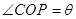 ,求
,求 面積的最大值及此時
面積的最大值及此時 的值.
的值.
(1)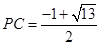 ;(2)
;(2)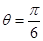 時,
時,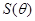 取得最大值為
取得最大值為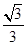 .
.
解析試題分析:本題考查解三角形中正弦定理、余弦定理的應(yīng)用,三角形面積公式以及運用三角公式進行恒等變形,考查學(xué)生的分析能力和計算能力.第一問,在 中,
中,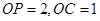 ,
,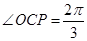 ,由余弦定理求邊長
,由余弦定理求邊長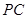 ;第二問,在
;第二問,在 中,利用正弦定理,得到
中,利用正弦定理,得到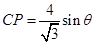 ,
,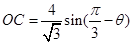 ,三角形面積公式
,三角形面積公式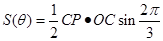 ,將上面2個邊長代入,利用二倍角公式、降冪公式、兩角和與差的正弦公式化簡表達式,再求三角函數(shù)的最值.
,將上面2個邊長代入,利用二倍角公式、降冪公式、兩角和與差的正弦公式化簡表達式,再求三角函數(shù)的最值.
試題解析:(1)在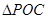 中,
中,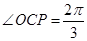 ,
,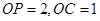 ,由
,由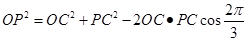 ,
,
得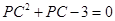 ,解得
,解得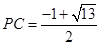 .
.
(2)∵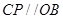 ,∴
,∴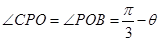 ,
,
在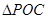 中,由正弦定理得
中,由正弦定理得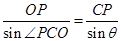 ,即
,即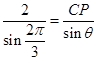 ,
,
∴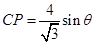 ,又
,又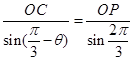 ,
,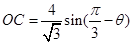 .
.
記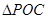 的面積為
的面積為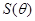 ,則
,則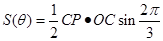
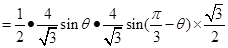
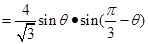
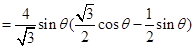
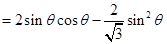
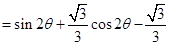
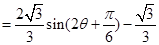
∴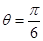 時,
時,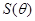 取得最大值為
取得最大值為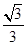 .
.
考點:1.余弦定理;2.正弦定理;3.二倍角公式;4.降冪公式;5.兩角和與差的正弦公式.


科目:高中數(shù)學(xué) 來源: 題型:解答題
已知二次函數(shù)f(x)=x2+ax(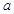
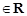 ).
).
(1)若函數(shù)y=f(sinx+ cosx)(
cosx)(
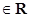 )的最大值為
)的最大值為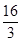 ,求f(x)的最小值;
,求f(x)的最小值;
(2)當(dāng)a>2時,求證:f(sin2xlog2sin2x+cos2xlog2cos2x)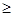 1–a.其中x∈R,x¹kp且x¹kp
1–a.其中x∈R,x¹kp且x¹kp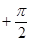 (k∈Z).
(k∈Z).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)
(1)當(dāng) 時,求
時,求 的最大值及相應(yīng)的x值;
的最大值及相應(yīng)的x值;
(2)利用函數(shù)y=sin 的圖象經(jīng)過怎樣的變換得到f(x)的圖象.
的圖象經(jīng)過怎樣的變換得到f(x)的圖象.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù) 的最大值為
的最大值為 ,且
,且 ,
, 是相鄰的兩對稱軸方程.
是相鄰的兩對稱軸方程.
(1)求函數(shù) 在
在 上的值域;
上的值域;
(2) 中,
中, ,角
,角 所對的邊分別是
所對的邊分別是 ,且
,且 ,
, ,求
,求 的面積.
的面積.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com