
【題目】已知定義在![]() 上的函數
上的函數![]() 是奇函數.
是奇函數.
(1)求![]() 的值;
的值;
(2)判斷![]() 的單調性,并用單調性定義證明;
的單調性,并用單調性定義證明;
(3)若對任意的![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() (2)
(2)![]() 在
在![]() 上是減函數(3)
上是減函數(3)![]()
【解析】試題分析:(1)由定義在實數集上的奇函數有![]() 列式求解,或直接由奇函數的定義得恒等式,由系數相等求解
列式求解,或直接由奇函數的定義得恒等式,由系數相等求解![]() 的值;(2)設
的值;(2)設![]() ,
, ![]() 且
且![]() ,可得
,可得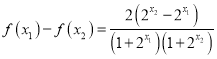 ,只需判斷
,只需判斷![]() ;(3)由函數的奇偶性和單調性,把給出的不等式轉化為含有
;(3)由函數的奇偶性和單調性,把給出的不等式轉化為含有![]() 的一元二次不等式,分離參數后求二次函數的最值,即可實數
的一元二次不等式,分離參數后求二次函數的最值,即可實數![]() 的取值范圍.
的取值范圍.
試題解析:(1)∵![]() 是定義在
是定義在![]() 上的奇函數,
上的奇函數,
∴![]() ,∴
,∴![]() ,∴
,∴![]() .
.
(2)![]() ,
, ![]() 在
在![]() 上是減函數.
上是減函數.
證明:設![]() ,
, ![]() 且
且![]() ,
,
則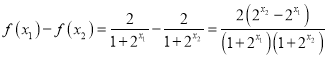 ,
,
∵![]() ,∴
,∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() ,
,
即![]() ,∴
,∴![]() 在
在![]() 上是減函數.
上是減函數.
(3)不等式![]()
![]()
又![]() 是
是![]() 上的減函數,∴
上的減函數,∴![]() ,
,
∴![]() ,對
,對![]() 恒成立,
恒成立,
∴![]() .
.
【方法點晴】本題主要考查函數的奇偶性及單調性的應用,以及不等式恒成立問題,屬于難題.不等式恒成立問題常見方法:① 分離參數![]() 恒成立(
恒成立(![]() 可)或
可)或![]() 恒成立(
恒成立(![]() 即可);② 數形結合(
即可);② 數形結合(![]() 圖象在
圖象在![]() 上方即可);③ 討論最值
上方即可);③ 討論最值![]() 或
或![]() 恒成立;④ 討論參數.
恒成立;④ 討論參數.


科目:高中數學 來源: 題型:
【題目】從裝有n+1個球(其中n個白球,1個黑球)的口袋中取出m個球(0<m≤n,m,n∈N),共有 ![]() 種取法.在這
種取法.在這 ![]() 種取法中,可以分成兩類:一類是取出的m個球全部為白球,共有
種取法中,可以分成兩類:一類是取出的m個球全部為白球,共有 ![]() 種取法;另一類是取出的m個球有m﹣1個白球和1個黑球,共有
種取法;另一類是取出的m個球有m﹣1個白球和1個黑球,共有 ![]() 種取法.顯然
種取法.顯然 ![]() ,即有等式:
,即有等式: ![]() 成立.試根據上述思想化簡下列式子:
成立.試根據上述思想化簡下列式子: ![]() = .
= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=loga(x+1)+loga(3﹣x)(a>0且a≠1),且f(1)=2
(1)求a的值及f(x)的定義域;
(2)若不等式f(x)≤c的恒成立,求實數c的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學用“五點法”畫函數![]() 在某一個周期內的圖像時,列表并填入了部分數據,如下表:
在某一個周期內的圖像時,列表并填入了部分數據,如下表:
| 0 |
|
|
|
|
|
|
|
|
|
|
| 0 | 5 | 0 | -5 | 0 |
(1)求出實數![]() ;
;
(2)求出函數![]() 的解析式;
的解析式;
(3)將![]() 圖像上所有點向左平移
圖像上所有點向左平移![]() 個單位長度,得到
個單位長度,得到![]() 圖像,求
圖像,求![]() 的圖像離原點
的圖像離原點![]() 最近的對稱中心.
最近的對稱中心.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】十二生肖,又叫屬相,是中國與十二地支相配以人出生年份的十二種動物,包括鼠、牛、虎、兔、龍、蛇、馬、羊、猴、雞、狗、豬。已知在甲、乙、丙、丁、戊、己六人中,甲、乙、丙的屬相均是龍,丁、戊的屬相均是虎,己的屬相是猴,現從這六人中隨機選出三人,則所選出的三人的屬相互不相同的概率等于( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某生產旅游紀念品的工廠,擬在2017年度進行系列促銷活動,經市場調查和測算,該紀念品的年銷售量 ![]() (單位:萬件)與年促銷費用
(單位:萬件)與年促銷費用 ![]() (單位:萬元)之間滿足
(單位:萬元)之間滿足 ![]() 于
于 ![]() 成反比例.若不搞促銷活動,紀念品的年銷售量只有1萬件.已知加工廠2017年生產紀念品的固定投資為3萬元,沒生產1萬件紀念品另外需要投資32萬元.當工廠把每件紀念品的售價定為“年平均每件生產成本的1.5倍”與“年平均每件所占促銷費的一半”之和時,則當年的產量和銷量相等.(利潤=收入-生產成本-促銷費用)
成反比例.若不搞促銷活動,紀念品的年銷售量只有1萬件.已知加工廠2017年生產紀念品的固定投資為3萬元,沒生產1萬件紀念品另外需要投資32萬元.當工廠把每件紀念品的售價定為“年平均每件生產成本的1.5倍”與“年平均每件所占促銷費的一半”之和時,則當年的產量和銷量相等.(利潤=收入-生產成本-促銷費用)
(Ⅰ)請把該工廠2017年的年利潤 ![]() (單位:萬元)表示成促銷費
(單位:萬元)表示成促銷費 ![]() (單位:萬元)的函數;
(單位:萬元)的函數;
(Ⅱ)試問:當2017年的促銷費投入多少萬元時,該工程的年利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一只小船以![]() 的速度由南向北勻速駛過湖面,在離湖面高20米的橋上,一輛汽車由西向東以
的速度由南向北勻速駛過湖面,在離湖面高20米的橋上,一輛汽車由西向東以![]() 的速度前進(如圖),現在小船在水平面上的
的速度前進(如圖),現在小船在水平面上的![]() 點以南的40米處,汽車在橋上
點以南的40米處,汽車在橋上![]() 點以西的30米處(其中
點以西的30米處(其中![]() 水平面),請畫出合適的空間圖形并求小船與汽車間的最短距離.(不考慮汽車與小船本身的大小).
水平面),請畫出合適的空間圖形并求小船與汽車間的最短距離.(不考慮汽車與小船本身的大小).

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}的前n項和為Sn , 且2Sn=(n+2)an﹣1(n∈N*).
(1)求a1的值;
(2)求數列{an}的通項公式;
(3)設Tn= ![]() ,求證:Tn<
,求證:Tn< ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com