
【題目】某高中社團進行社會實踐,對[25,55]歲的人群隨機抽取n人進行了一次是否開通“微博”的調查,若開通“微博”的稱為“時尚族”,否則稱為“非時尚族”,通過調查分別得到如圖所示統計表和各年齡段人數頻率分布直方圖: 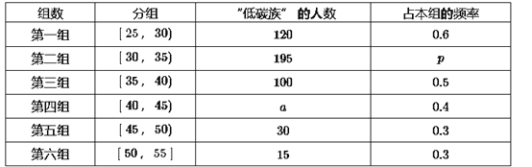
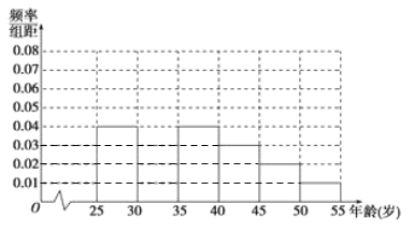
完成以下問題:
(Ⅰ)補全頻率分布直方圖并求n,a,p的值;
(Ⅱ)從[40,50)歲年齡段的“時尚族”中采用分層抽樣法抽取18人參加網絡時尚達人大賽,其中選取3人作為領隊,記選取的3名領隊中年齡在[40,45)歲的人數為X,求X的分布列和期望E(X)..
【答案】(1)直方圖見解析,![]() (2)分布列見解析,
(2)分布列見解析,![]()
【解析】
試題(Ⅰ)根據所求矩形的面積和為1求出第二組的頻率,然后求出高,畫出頻率直方圖,求出第一組的人數和頻率從而求出n,由題可知,第二組的頻率以及人數,從而求出p的值,然后求出第四組的頻率和人數從而求出a的值;
(Ⅱ)因為[40,45)歲年齡段的“時尚族”與[45,50)歲年齡段的“時尚族”的比值為2:1,所以采用分層抽樣法抽取18人,[40,45)歲中有12人,[45,50)歲中有6人,機變量X服從超幾何分布,X的取值可能為0,1,2,3,分別求出相應的概率,列出分布列,根據數學期望公式求出期望即可.
試題解析:解:(Ⅰ)第二組的頻率為1-(0.04+0.04+0.03+0.02+0.01)×5=0.3,
所以高為![]() . 頻率直方圖如下:
. 頻率直方圖如下:
第一組的人數為![]() ,頻率為0.04×5=0.2,所以
,頻率為0.04×5=0.2,所以![]() .
.
由題可知,第二組的頻率為0.3,所以第二組的人數為1000×0.3=300, 所以![]() .
.
第四組的頻率為0.03×5=0.15,所以第四組的人數為1000×0.15=150, 所以a=150×0.4=60.
(Ⅱ)因為[40,45)歲年齡段的“時尚族”與[45,50)歲年齡段的“時尚族”的比值
為60:30=2:1,所以采用分層抽樣法抽取18人,[40,45)歲中有12人,[45,50)歲中有6人.
隨機變量X服從超幾何分布.![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以隨機變量X的分布列為
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
∴數學期望![]() (或者
(或者 ![]() ).
).


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() ,
,![]() ,
,![]() ,給出以下四個命題:①
,給出以下四個命題:①![]() 為偶函數;②
為偶函數;②![]() 為偶函數;③
為偶函數;③![]() 的最小值為0;④
的最小值為0;④![]() 有兩個零點.其中真命題的是( ).
有兩個零點.其中真命題的是( ).
A.②④B.①③C.①③④D.①④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() .其中
.其中![]() ,
,![]() 表示直線,
表示直線,![]() 、β表示平面,給出如下5個命題:
、β表示平面,給出如下5個命題:
①若![]() //
//![]() ,則
,則![]() //
//![]() ;
;
②若![]() ⊥
⊥![]() ,則
,則![]() ⊥
⊥![]() ;
;
③![]() 與
與![]() 不垂直,則
不垂直,則![]() 不可能成立;
不可能成立;
④若![]() ,則
,則![]() ;
;
⑤![]() ,則
,則![]() ;
;
其中真命題的個數是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為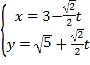 (
(![]() 為參數),在以坐標原點
為參數),在以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸的極坐標中,圓
軸正半軸為極軸的極坐標中,圓![]() 的方程為
的方程為![]() .
.
(1)寫出直線![]() 的普通方程和圓
的普通方程和圓![]() 的直角坐標方程;
的直角坐標方程;
(2)若點![]() 的坐標為
的坐標為![]() ,圓
,圓![]() 與直線
與直線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 年,某省將實施新高考,
年,某省將實施新高考,![]() 年秋季入學的高一學生是新高考首批考生,新高考不再分文理科,采用
年秋季入學的高一學生是新高考首批考生,新高考不再分文理科,采用![]() 模式,其中語文、數學、外語三科為必考科目,滿分各
模式,其中語文、數學、外語三科為必考科目,滿分各![]() 分,另外,考生還要依據想考取的高校及專業的要求,結合自己的興趣愛好等因素,在思想政治、歷史、地理、物理、化學、生物
分,另外,考生還要依據想考取的高校及專業的要求,結合自己的興趣愛好等因素,在思想政治、歷史、地理、物理、化學、生物![]() 門科目中自選
門科目中自選![]() 門參加考試(
門參加考試(![]() 選
選![]() ),每科目滿分
),每科目滿分![]() 分.為了應對新高考,某高中從高一年級
分.為了應對新高考,某高中從高一年級![]() 名學生(其中男生
名學生(其中男生![]() 人,女生
人,女生![]() 人)中,采用分層抽樣的方法從中抽取n名學生進行調查.
人)中,采用分層抽樣的方法從中抽取n名學生進行調查.
(1)已知抽取的n名學生中含女生![]() 人,求n的值及抽取到的男生人數;
人,求n的值及抽取到的男生人數;
(2)學校計劃在高一上學期開設選修中的“物理”和“歷史”兩個科目,為了了解學生對這兩個科目的選課情況,對在(1)的條件下抽取到的![]() 名學生進行問卷調查(假定每名學生在這兩個科目中必須選擇一個科目且只能選擇一個科目),下面表格是根據調查結果得到的
名學生進行問卷調查(假定每名學生在這兩個科目中必須選擇一個科目且只能選擇一個科目),下面表格是根據調查結果得到的![]() 列聯表,請將下面的列聯表補充完整,并判斷是否有
列聯表,請將下面的列聯表補充完整,并判斷是否有![]() 的把握認為選擇科目與性別有關?說明你的理由;
的把握認為選擇科目與性別有關?說明你的理由;
選擇“物理” | 選擇“歷史” | 總計 | |
男生 | 10 | ||
女生 | 30 | ||
總計 |
(3)在抽取到的![]() 名女生中,在(2)的條件下,按選擇的科目進行分層抽樣,抽出
名女生中,在(2)的條件下,按選擇的科目進行分層抽樣,抽出![]() 名女生,了解女生對“歷史”的選課意向情況,在這
名女生,了解女生對“歷史”的選課意向情況,在這![]() 名女生中再抽取
名女生中再抽取![]() 人,求這
人,求這![]() 人中選擇“歷史”的人數為
人中選擇“歷史”的人數為![]() 人的概率.
人的概率.
參考數據:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式: ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為坐標原點,橢圓
為坐標原點,橢圓![]() 的離心率為
的離心率為![]() ,雙曲線
,雙曲線![]() 的漸近線與橢圓
的漸近線與橢圓![]() 的交點到原點的距離均為
的交點到原點的距離均為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若點![]() 為橢圓
為橢圓![]() 上的動點,
上的動點,![]() 三點共線,直線
三點共線,直線![]() 的斜率分別為
的斜率分別為![]() .
.
(i)證明:![]() ;
;
(ii)若![]() ,設直線
,設直線![]() 過點
過點![]() ,直線
,直線![]() 過點
過點![]() ,證明:
,證明:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,點![]() 是以
是以![]() 為直徑的圓上的動點(異于
為直徑的圓上的動點(異于![]() ,
,![]() ),已知
),已知![]() ,
,![]() ,
,![]() 平面
平面![]() ,四邊形
,四邊形![]() 為平行四邊形.
為平行四邊形.
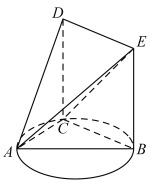
(1)求證:![]() 平面
平面![]() ;
;
(2)當三棱錐![]() 的體積最大時,求平面
的體積最大時,求平面![]() 與平面
與平面![]() 所成的銳二面角的余弦值.
所成的銳二面角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】垃圾分類是對垃圾進行有效處置的一種科學管理方法,為了了解居民對垃圾分類的知曉率和參與率,引導居民積極行動,科學地進行垃圾分類,某小區隨機抽取年齡在區間[25,85]上的50人進行調研,統計出年齡頻數分布及了解垃圾分類的人數如表:

(1)填寫下面2x2列聯表,并判斷能否在犯錯誤的概率不超過0.01的前提下認為以65歲為分界點居民對了解垃圾分類的有關知識有差異;
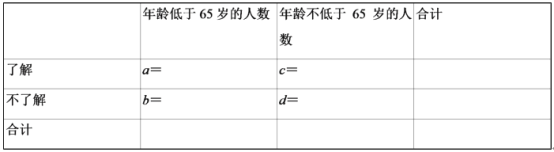
(2)若對年齡在[45,55),[25,35)的被調研人中各隨機選取2人進行深入調研,記選中的4人中不了解垃圾分類的人數為X,求隨機變量X的分布列和數學期望.
參考公式和數據K2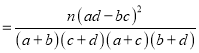 ,其中n=a+b+c+d.
,其中n=a+b+c+d.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com