
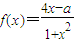 在區間[m,n]上為增函數,且f(m)f(n)=-4.
在區間[m,n]上為增函數,且f(m)f(n)=-4. ,證明:x1<x<x2.
,證明:x1<x<x2.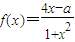 在區間[m,n]上為增函數,先用導數求得當a=3時的所有單調區間,則有[m,n]為函數f(x)單調區間的子集.
在區間[m,n]上為增函數,先用導數求得當a=3時的所有單調區間,則有[m,n]為函數f(x)單調區間的子集.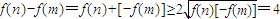 ,當且僅當f(n)=-f(m)=2時等號成立求解.
,當且僅當f(n)=-f(m)=2時等號成立求解.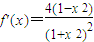 和
和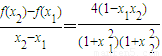 ,再由
,再由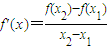 ,得到,
,得到,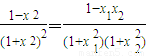 ,再用作差法比較
,再用作差法比較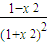 與
與 的大小.
的大小.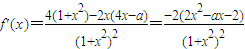 .(2分)
.(2分)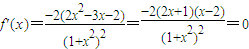 ,
,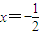 或x=2,
或x=2,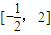 上為增函數,在
上為增函數,在 ,(2,+∞)上為減函數,(4分)
,(2,+∞)上為減函數,(4分)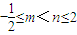 ,且
,且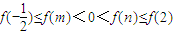 .
.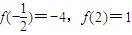 ,所以
,所以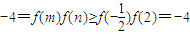 ,
, .(7分)
.(7分)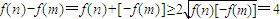 ,
,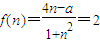 ,有-a=2(n-1)2≥0,得a≤0;(9分)
,有-a=2(n-1)2≥0,得a≤0;(9分)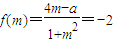 ,有a=2(m+1)2≥0,得a≥0;(10分)
,有a=2(m+1)2≥0,得a≥0;(10分)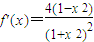 ,
,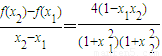 ,
,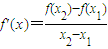 知,
知,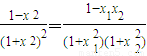 ,(12分)
,(12分)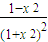 與
與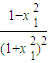 的大小.
的大小.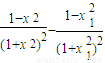
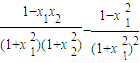
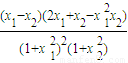
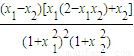
 ,(13分)
,(13分)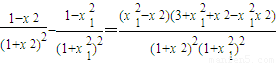 ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源:2009-2010學年湖北省部分重點中學聯考高三(上)期中數學試卷(理科)(解析版) 題型:選擇題
 在區間M上的反函數是其本身,則M可以是( )
在區間M上的反函數是其本身,則M可以是( )查看答案和解析>>
科目:高中數學 來源:2010年重慶市部分重點中學高考數學一模試卷(理科)(解析版) 題型:選擇題
 在區間M上的反函數是其本身,則M可以是( )
在區間M上的反函數是其本身,則M可以是( )查看答案和解析>>
科目:高中數學 來源:2010年山東省高考數學押題試卷(理科)(解析版) 題型:解答題
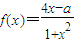 在區間[m,n]上為增函數,且f(m)f(n)=-4.
在區間[m,n]上為增函數,且f(m)f(n)=-4. ,證明:x1<x<x2.
,證明:x1<x<x2.查看答案和解析>>
科目:高中數學 來源:2007年北京市朝陽區高考數學一模試卷(理科)(解析版) 題型:選擇題
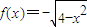 在區間M上的反函數是其本身,則M可以是( )
在區間M上的反函數是其本身,則M可以是( )查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com