
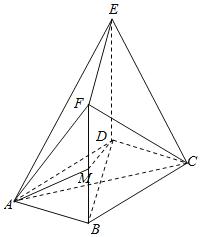
【題目】如圖,在多面體ABCDEF中,底面ABCD是邊長為2的菱形,∠BAD=60°,四邊形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M為線段BF上一點,且DM⊥平面ACE.
(1)求BM的長;
(2)求二面角A﹣DM﹣B的余弦值的大小.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根據DM⊥平面ACE,找出線線垂直,在平面四邊形EFBD中根據垂直關系求得線段長度;
(2)由題可知直線![]() 垂直于平面
垂直于平面![]() ,故可過
,故可過![]() 與
與![]() 中點作
中點作![]() 垂線,找到二面角的平面角,從而在三角形中求解角度的大小即可.
垂線,找到二面角的平面角,從而在三角形中求解角度的大小即可.
(1)記![]() 與
與![]() 的交點為
的交點為![]() ,連接
,連接![]() ,如下圖所示:
,如下圖所示:
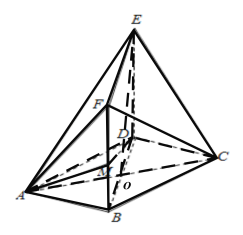
因為![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
故![]() ,
,
又因為![]() //
//![]() ,可以確定一個平面,故
,可以確定一個平面,故![]() 均在平面
均在平面![]() 中;
中;
因為四邊形![]() 是菱形,且
是菱形,且![]() ,故可得
,故可得![]() ;
;
故在矩形![]() 中:
中:
因為![]() ,故可得
,故可得![]() ,
,
又因為![]() ,
,![]() ,
,
故可得![]() ,故可得
,故可得![]() .
.
即![]() .
.
(2)記![]() 與
與![]() 的交點為
的交點為![]() ,連接
,連接![]() ,如下圖所示:
,如下圖所示:
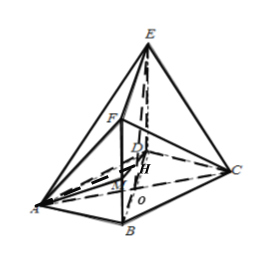
因為四邊形![]() 為菱形,故可得
為菱形,故可得![]() ,
,
又因為平面BDEF⊥平面ABCD,且平面BDEF![]() 平面ABCD
平面ABCD![]()
且![]() 平面
平面![]() ,
,![]() ,
,
故可得![]() 平面
平面![]() ;
;
由(1)可知![]() ,故
,故![]() 即為二面角A﹣DM﹣B的平面角;
即為二面角A﹣DM﹣B的平面角;
在![]() 中,容易知
中,容易知![]() ,故
,故![]()
在![]() 中,又
中,又![]() ,解得
,解得![]() ;
;
在菱形![]() 中,容易知
中,容易知![]() .
.
故在![]() 中,因為
中,因為![]() ,
,![]() ,故由勾股定理可得
,故由勾股定理可得![]() ,
,
故![]() .
.
二面角A﹣DM﹣B的余弦值的大小為![]() .
.


 一線名師權威作業本系列答案
一線名師權威作業本系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數且
為參數且 ![]() )曲線
)曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,且
為參數,且![]() ),以
),以![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為:
的極坐標方程為:![]() ,曲線
,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 與
與![]() 的交點到極點的距離;
的交點到極點的距離;
(2)設![]() 與
與![]() 交于
交于![]() 點,
點,![]() 與
與![]() 交于
交于![]() 點,當
點,當![]() 在
在![]() 上變化時,求
上變化時,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業打算處理一批產品,這些產品每箱100件,以箱為單位銷售.已知這批產品中每箱出現的廢品率只有![]() 或者
或者![]() 兩種可能,兩種可能對應的概率均為0.5.假設該產品正品每件市場價格為100元,廢品不值錢.現處理價格為每箱8400元,遇到廢品不予更換.以一箱產品中正品的價格期望值作為決策依據.
兩種可能,兩種可能對應的概率均為0.5.假設該產品正品每件市場價格為100元,廢品不值錢.現處理價格為每箱8400元,遇到廢品不予更換.以一箱產品中正品的價格期望值作為決策依據.
(1)在不開箱檢驗的情況下,判斷是否可以購買;
(2)現允許開箱,有放回地隨機從一箱中抽取2件產品進行檢驗.
①若此箱出現的廢品率為![]() ,記抽到的廢品數為
,記抽到的廢品數為![]() ,求
,求![]() 的分布列和數學期望;
的分布列和數學期望;
②若已發現在抽取檢驗的2件產品中,其中恰有一件是廢品,判斷是否可以購買.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為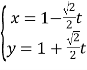 (
(![]() 為參數),以坐標原點為極點,以
為參數),以坐標原點為極點,以![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 與
與![]() 交于
交于![]() 兩點,點
兩點,點![]() 的極坐標為
的極坐標為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學將100名高一新生分成水平相同的甲,乙兩個“平行班”,每班50人.陳老師采用A,B兩種不同的教學方式分別在甲,乙兩個班級進行教改實驗.為了解教學效果,期末考試后,陳老師分別從兩個班級中各隨機抽取20名學生的成績進行統計,作出莖葉圖如下,計成績不低于90分者為“成績優秀”.

(1)從乙班樣本的20個個體中,從不低于86分的成績中隨機抽取2個,求抽出的兩個均“成績優秀”的概率;
(2)由以上統計數據填寫下面2x2列聯表,并判斷是否有![]() 的把握認為“成績優秀”與教學方式有關.
的把握認為“成績優秀”與教學方式有關.
甲班(A方式) | 乙班(B方式) | 總計 | |
成績優秀 | |||
成績不優秀 | |||
總計 |
附: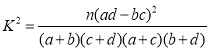
P( | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | /tr>
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy下,曲線C1的參數方程為![]() (
(![]() 為參數),曲線C1在變換T:
為參數),曲線C1在變換T:![]() 的作用下變成曲線C2.
的作用下變成曲線C2.
(1)求曲線C2的普通方程;
(2)若m>1,求曲線C2與曲線C3:y=m|x|-m的公共點的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 經過點
經過點![]() ,右焦點到直線
,右焦點到直線![]() 的距離為
的距離為![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)定義![]() 為
為![]() ,
,![]() 兩點所在直線的斜率,若四邊形
兩點所在直線的斜率,若四邊形![]() 為橢圓的內接四邊形,且
為橢圓的內接四邊形,且![]() ,
,![]() 相交于原點
相交于原點![]() ,且
,且![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著經濟水平及個人消費能力的提升,我國居民對精神層面的追求愈加迫切,如圖是2007年到2017年我國城鎮居民教育、文化、服務人均消費支出同比增速的折線圖,圖中顯示2007年的同比增速為10%, 即2007年與2006年同時期比較2007年的人均消費支出費用是2006年的1.1倍.則下列表述中正確的是( )
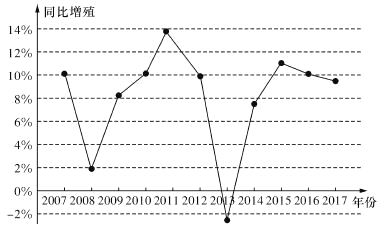
A.2007年到2017年,同比增速的中位數約為10%
B.2007年到2017年,同比增速的極差約為12%
C.2011年我國城鎮居民教育、文化、服務人均消費支出的費用最高
D.2007年到2017年,我國城鎮居民教育、文化、服務人均消費支出的費用逐年增加
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com