【題目】已知橢圓
的長軸長為
，焦距為2，拋物線
的準線經過
的左焦點
.
（1）求與
的方程；
（2）直線
經過的上頂點且與交于
，
兩點，直線
，
與分別交于點
（異于點），
（異于點），證明：直線
的斜率為定值.
名校課堂系列答案科目：高中數學 來源： 題型：
【題目】已知直線
的參數方程為
為參數），以坐標原點為極點，
軸的正半軸為極軸建立極坐標系，曲線
的極坐標方程為
.
（1）求直線的普通方程和曲線的直角坐標方程；
（2）設點
，直線與曲線交于
兩點，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】
對函數Φ（x），定義fk（x）＝Φ（x－mk）＋nk（其中x∈（mk，m＋mk]，k∈Z，m＞0，n＞0，且m、n為常數）為Φ（x）的第k階階梯函數，m叫做階寬，n叫做階高，已知階寬為2，階高為3．
（1）當Φ（x）＝2x時 ①求f0（x）和fk（x）的解析式； ②求證：Φ（x）的各階階梯函數圖象的最高點共線；
（2）若Φ（x）＝x2，則是否存在正整數k，使得不等式fk（x）＜（1－3k）x＋4k2＋3k－1有解？若存在，求出k的值；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某班級有3名同學報名參加學校組織的辯論賽，現有甲、乙兩個辨題可以選擇，學校決定讓選手以抽取卡片（除上面標的數不同外其他完全相同）的方式選擇辯題，且每名選手抽取后放回．已知共有10張卡片，卡片上分別標有
共10個數．若抽到卡片上的數為質數（2，3，5，7），則選擇甲辨題，否則選擇乙辯題．
（1）求這3名同學中至少有1人選擇甲辨題的概率．
（2）用X、Y分別表示這3名同學中選擇甲、乙辨題的人數，求
的分布列和數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓方程
（
），
，
是橢圓的左右焦點，以，及橢圓短軸的一個端點為頂點的三角形是面積為
的正三角形.
（1）求橢圓方程；
（2）過分別作直線
，
，且
，設與橢圓交于
，
兩點，與橢圓交于
，
兩點，求四邊形
面積的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】撫州市某中學利用周末組織教職員工進行了一次秋季登軍峰山健身的活動，有
人參加，現將所有參加人員按年齡情況分為
，
，
，
，
，
，
等七組，其頻率分布直方圖如下圖所示．已知之間的參加者有4人．
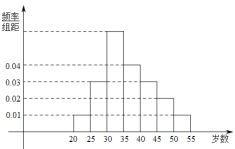
（1）求和之間的參加者人數
；
（2）組織者從
之間的參加者（其中共有
名女教師包括甲女，其余全為男教師）中隨機選取
名擔任后勤保障工作，求在甲女必須入選的條件下，選出的女教師的人數為2人的概率.
（3）已知和之間各有
名數學教師，現從這兩個組中各選取人擔任接待工作，設兩組的選擇互不影響，求兩組選出的人中都至少有
名數學教師的概率?
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】學校為了對教師教學水平和教師管理水平進行評價，從該校學生中選出300人進行統計.其中對教師教學水平給出好評的學生人數為總數的
，對教師管理水平給出好評的學生人數為總數的
，其中對教師教學水平和教師管理水平都給出好評的有120人.
（1）填寫教師教學水平和教師管理水平評價的
列聯表：
對教師管理水平好評 | 對教師管理水平不滿意 | 合計 | |
對教師教學水平好評 | |||
對教師教學水平不滿意 | |||
合計 |
請問是否可以在犯錯誤概率不超過0.001的前提下，認為教師教學水平好評與教師管理水平好評有關？
（2）若將頻率視為概率，有4人參與了此次評價，設對教師教學水平和教師管理水平全好評的人數為隨機變量
.
①求對教師教學水平和教師管理水平全好評的人數的分布列（概率用組合數算式表示）；
②求的數學期望和方差.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（
，其中
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對相關系數r來說，下列說法正確的是（ ）.
A.
，
越接近0，相關程度越大；越接近1，相關程度越小
B.
，越接近1，相關程度越大；越大，相關程度越小
C.，越接近1，相關程度越大；越接近0，相關程度越小
D.，越接近1，相關程度越小；越大，相關程度越大
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
