
(1)設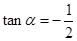 ,求
,求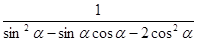 的值;
的值;
(2)已知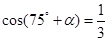 ,且
,且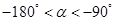 ,求
,求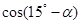 的值.
的值.
(1) ;(2)
;(2) .
.
【解析】
試題分析:(1)將所求式分子1換成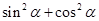 ,然后分子分母同除以
,然后分子分母同除以 ,將其轉化為關于
,將其轉化為關于 的式子再進行計算即可,本題若由
的式子再進行計算即可,本題若由 ,去求出
,去求出 ,則需要討論,若想不到用
,則需要討論,若想不到用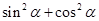 代替1,則可原式分子分母同除以
代替1,則可原式分子分母同除以 ,然后再考慮求出
,然后再考慮求出 ,顯然這兩種方法較為麻煩;(2)此類給三角函數值求三角函數值的問題一般是通過考察條件中的角和問題中的角的關系,然后通過誘導公式、同角三角函數關系式、和差角公式進行計算.注意到
,顯然這兩種方法較為麻煩;(2)此類給三角函數值求三角函數值的問題一般是通過考察條件中的角和問題中的角的關系,然后通過誘導公式、同角三角函數關系式、和差角公式進行計算.注意到 ,由誘導公式知
,由誘導公式知 ,結合條件由同角三角函數關系式可求出
,結合條件由同角三角函數關系式可求出 ,注意公式使用時要考察角的范圍從而確定三角函數值的符號.
,注意公式使用時要考察角的范圍從而確定三角函數值的符號.
試題解析:(1)原式= 3分
3分
 7分
7分
(2)由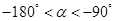 ,得
,得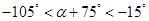 ,
,
故 10分
10分
而
所以 14分
14分
考點:同角三角函數的關系、三角函數的誘導公式.


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com