【題目】在平面直角坐標系
中,點
,直線
,設圓
的半徑為1且關于直線l對稱.
(1)若圓心在直線
上,過點
作圓的切線,求切線的方程；
(2)點
關于點
的對稱點為B，若圓上存在點
,使
,求圓心的橫坐標
的取值范圍.
【答案】(1) 
;(2) 
.
【解析】試題分析：（1）先求出圓心坐標，可得圓的方程，再設出切線方程，利用點到直線的距離公式，即可求得切線方程；
（2）設出點C，M的坐標，利用
，尋找坐標之間的關系，進一步將問題轉化為圓與圓的位置關系，即可得出結論．
(1)由
得圓心C為(1,-4),∵圓C的半徑為1
∴圓C的方程為: 
顯然切線的斜率一定存在,設所求圓C的切線方程為
,即
∴
∴
∴所求圓C的切線方程為: 
或者
(2)依題意求得B(-1,1)
∵圓C的圓心在在直線
上,所以,設圓心C為(a,a-5)
又∵
∴設M為(x,y)，則
整理得: 
設為圓D
∴點M應該既在圓C上又在圓D上，即圓C和圓D有交點
∴
∴
由
得
由
得
終上所述,a的取值范圍為: 
三點一測快樂周計劃系列答案科目：高中數學 來源： 題型：
【題目】交通指數是交通擁堵指數的簡稱，是綜合反映道路網暢通或擁堵的概念，記交通指數為
，其范圍為
，分為五個級別， 
暢通； 
基本暢通； 
輕度擁堵； 
中度擁堵； 
嚴重擁堵.早高峰時段（
），從某市交通指揮中心隨機選取了三環以內的50個交通路段，依據其交通指數數據繪制的頻率分布直方圖如圖.
（1）這50個路段為中度擁堵的有多少個？
（2）據此估計，早高峰三環以內的三個路段至少有一個是嚴重擁堵的概率是多少？
（3）某人上班路上所用時間若暢通時為20分鐘，基本暢通為30分鐘，輕度擁堵為36分鐘，中度擁堵為42分鐘，嚴重擁堵為60分鐘，求此人所用時間的數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知動圓
過定點
且與圓
相切，記動圓圓心
的軌跡為曲線
.
（1）求曲線
的方程；
（2）過點
且斜率不為零的直線交曲線
于
， 
兩點，在
軸上是否存在定點
，使得直線
的斜率之積為非零常數？若存在，求出定點的坐標；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（文科）某出租車公司響應國家節能減排的號召，已陸續購買了140輛純電動汽車作為運營車輛，目前我國主流純電動汽車按續駛里程數
（單位：公里）分為3類，即
， 
， 
.對這140輛車的行駛總里程進行統計，結果如下表：
（1）從這140輛汽車中任取1輛，求該車行駛總里程超過5萬公里的概率； （2）公司為了了解這些車的工作狀況，決定抽取14輛車進行車況分析，按表中描述的六種情況進行分層抽樣，設從
類車中抽取了
輛車. （ⅰ）求
的值； （ⅱ）如果從這
輛車中隨機選取2輛車，求恰有1輛車行駛總里程超過5萬公里的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題共l2分）
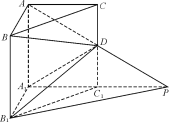
如圖，在直三棱柱ABC－A1B1C1中，∠BAC=90°，AB=AC=AA1=1，延長A1C1至點P，使C1P＝A1C1，連接AP交棱CC1于D．
（Ⅰ）求證：PB1∥平面BDA1；
（Ⅱ）求二面角A－A1D－B的平面角的余弦值；
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
