
【題目】已知圓![]() ,直線
,直線![]() 過點
過點![]() .
.
(1)若直線![]() 與圓
與圓![]() 相切,求直線
相切,求直線![]() 的方程;
的方程;
(2)若直線![]() 與圓
與圓![]() 交于
交于![]() 兩點,當
兩點,當![]() 的面積最大時,求直線
的面積最大時,求直線![]() 的方程.
的方程.
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)分直線l的斜率不存在與直線l的斜率存在兩種討論,根據直線l與圓M相切進行計算,可得直線![]() 的方程;
的方程;
(2)設直線l的方程為![]() ,圓心到直線l的距離為d,可得
,圓心到直線l的距離為d,可得![]() 的長,由
的長,由![]() 的面積最大,可得
的面積最大,可得![]() ,可得k的值,可得直線
,可得k的值,可得直線![]() 的方程.
的方程.
解:(1)當直線l的斜率不存在時,直線l的方程為![]() ,此時直線l與圓M相切,所以
,此時直線l與圓M相切,所以![]() 符合題意 ,
符合題意 ,
當直線l的斜率存在時,設l的斜率為k,
則直線l的方程為![]() ,
,
即![]() ,
,
因為直線l與圓M相切,所以圓心到直線的距離等于圓的半徑,
即![]() ,
,
解得![]() ,即直線l的方程為
,即直線l的方程為![]() ;
;
綜上,直線l的方程為![]() 或
或![]() ,
,
(2)因為直線l與圓M交于P.Q兩點,所以直線l的斜率存在,
可設直線l的方程為![]() ,圓心到直線l的距離為d ,
,圓心到直線l的距離為d ,
則![]() ,
,
從而![]() 的面積為
的面積為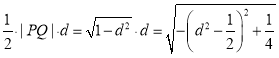 ·
·
當![]() 時,
時,![]() 的面積最大 ,
的面積最大 ,
因為![]() ,
,
所以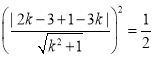 ,
,
解得![]() 或
或![]() ,
,
故直線l的方程為![]() 或
或![]() .
.


科目:高中數學 來源: 題型:
【題目】某蛋糕店每天做若干個生日蛋糕,每個制作成本為50元,當天以每個100元售出,若當天白天售不出,則當晚以30元/個價格作普通蛋糕低價售出,可以全部售完.
(1)若蛋糕店每天做20個生日蛋糕,求當天的利潤![]() (單位:元)關于當天生日蛋糕的需求量
(單位:元)關于當天生日蛋糕的需求量![]() (單位:個,
(單位:個, ![]() )的函數關系;
)的函數關系;
(2)蛋糕店記錄了100天生日蛋糕的日需求量(單位:個)整理得下表:

(ⅰ)假設蛋糕店在這100天內每天制作20個生日蛋糕,求這100天的日利潤(單位:元)的平均數;
(ⅱ)若蛋糕店一天制作20個生日蛋糕,以100天記錄的各需求量的頻率作為概率,求當天利潤不少于900元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】眉山市位于四川西南,有“千載詩書城,人文第一州”的美譽,這里是大文豪蘇軾、蘇洵、蘇轍的故鄉,也是人們旅游的好地方.在今年的國慶黃金周,為了豐富游客的文化生活,每天在東坡故里三蘇祠舉行“三蘇文化”知識競賽.已知甲、乙兩隊參賽,每隊3人,每人回答一個問題,答對者為本隊贏得一分,答錯得零分.假設甲隊中每人答對的概率均為![]() ,乙隊中3人答對的概率分別為
,乙隊中3人答對的概率分別為![]() ,
,![]() ,
,![]() ,且各人回答正確與否相互之間沒有影響.
,且各人回答正確與否相互之間沒有影響.
(1)分別求甲隊總得分為0分;2分的概率;
(2)求甲隊得2分乙隊得1分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|2≤x≤8},B={x|1<x<6},C={x|x>a},U=R.
(1)求A∪B,(CUA)∩B;
(2)若A∩C≠![]() ,求a的取值范圍.
,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列{an}滿足a1= ![]() ,an+1﹣1=an(an﹣1)(n∈N*)且Sn=
,an+1﹣1=an(an﹣1)(n∈N*)且Sn= ![]() +
+ ![]() +…+
+…+ ![]() ,則Sn的整數部分的所有可能值構成的集合是( )
,則Sn的整數部分的所有可能值構成的集合是( )
A.{0,1,2}
B.{0,1,2,3}
C.{1,2}
D.{0,2}
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知AB是⊙O的直徑,點D是⊙O上一點,過點D作⊙O的切線,交AB的延長線于點C,過點C作AC的垂線,交AD的延長線于點E. 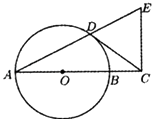
(1)求證:△CDE為等腰三角形;
(2)若AD=2, ![]() =
= ![]() ,求⊙O的面積.
,求⊙O的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com