
【題目】已知函數![]() .
.
(1)若曲線![]() 過點
過點![]() ,求曲線
,求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)求函數![]() 在區間
在區間![]() 上的最大值;
上的最大值;
(3)若函數![]() 有兩個不同的零點
有兩個不同的零點![]() ,
, ![]() ,求證:
,求證: ![]() .
.
【答案】(1)![]() ;(2)當
;(2)當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ;(3)證明見解析.
;(3)證明見解析.
【解析】試題分析:(1)因為點![]() 在曲線
在曲線![]() 上,所以
上,所以![]() ,解得
,解得![]() ,利用導數求得斜率為
,利用導數求得斜率為![]() ,故切線為
,故切線為![]() ;(2)
;(2)![]() ,將
,將![]() 分成
分成![]() 四類,討論函數的單調區間進而求得最大值;(3)不妨設
四類,討論函數的單調區間進而求得最大值;(3)不妨設![]() ,因為
,因為![]() ,所以
,所以![]() ,
,![]() ,要證明
,要證明![]() ,即證明
,即證明![]() ,令
,令![]() ,即證
,即證![]() ,令
,令![]() (
(![]() ),利用導數求得
),利用導數求得![]() 的最小值大于零即可.
的最小值大于零即可.
試題解析:
(1)因為點![]() 在曲線
在曲線![]() 上,所以
上,所以![]() ,解得
,解得![]() .
.
因為![]() ,所以切線的斜率為0,
,所以切線的斜率為0,
所以切線方程為![]() .
.
(2)因為![]() ,
,
①當![]() 時,
時, ![]() ,
, ![]() ,
,
所以函數![]() 在
在![]() 上單調遞增,則
上單調遞增,則![]() ;
;
②當![]() ,即
,即![]() 時,
時, ![]() ,
, ![]() ,
,
所以函數![]() 在
在![]() 上單調遞增,則
上單調遞增,則![]() ;
;
③當![]() ,即
,即![]() 時,
時,
函數![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
則![]() ;
;
④當![]() ,即
,即![]() 時,
時, ![]() ,
, ![]() ,
,
函數![]() 在
在![]() 上單調遞減,則
上單調遞減,則![]() .
.
綜上,當![]() 時,
時, ![]() ;
;
當![]() 時,
時, ![]() ;
;
當![]() 時,
時, ![]() .
.
(3)不妨設![]() ,
,
因為![]() ,
,
所以![]() ,
,![]() ,
,
可得![]() ,
, ![]() ,
,
要證明![]() ,即證明
,即證明![]() ,也就是
,也就是![]() ,
,
因為![]() ,
,
所以即證明![]() ,
,
即![]() ,
,
令![]() ,則
,則![]() ,于是
,于是![]() ,
,
令![]() (
(![]() ),
),
則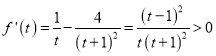 ,
,
故函數![]() 在
在![]() 上是增函數,
上是增函數,
所以![]() ,即
,即![]() 成立,所以原不等式成立.
成立,所以原不等式成立.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數學 來源: 題型:
【題目】已知點![]() ,橢圓
,橢圓![]() 的離心率為
的離心率為![]() 是橢圓的焦點,直線
是橢圓的焦點,直線![]() 的斜率為
的斜率為![]() 為坐標原點.
為坐標原點.
(1)求橢圓![]() 的方程;
的方程;
(2)設過點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,當
兩點,當![]() 的面積最大時,求直線
的面積最大時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ).
).
(1)若曲線![]() 在點
在點![]() 處的切線經過點
處的切線經過點![]() ,求
,求![]() 的值;
的值;
(2)若![]() 在區間
在區間![]() 上存在極值點,判斷該極值點是極大值點還是極小值點,并求
上存在極值點,判斷該極值點是極大值點還是極小值點,并求![]() 的取值范圍;
的取值范圍;
(3)若當![]() 時,
時, ![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設某物體一天中的溫度![]() 是時間
是時間![]() 的函數,已知
的函數,已知![]() ,其中溫度的單位是
,其中溫度的單位是![]() ,時間的單位是小時,規定中午12:00相應的
,時間的單位是小時,規定中午12:00相應的![]() ,中午12:00以后相應的
,中午12:00以后相應的![]() 取正數,中午12:00以前相應的
取正數,中午12:00以前相應的![]() 取負數(例如早上8:00相應的
取負數(例如早上8:00相應的![]() ,下午16:00相應的
,下午16:00相應的![]() ),若測得該物體在中午12:00的溫度為
),若測得該物體在中午12:00的溫度為![]() ,在下午13:00的溫度為
,在下午13:00的溫度為![]() ,且已知該物體的溫度在早上8:00與下午16:00有相同的變化率.
,且已知該物體的溫度在早上8:00與下午16:00有相同的變化率.
(1)求該物體的溫度![]() 關于時間
關于時間![]() 的函數關系式;
的函數關系式;
(2)該物體在上午10:00至下午14:00這段時間中(包括端點)何時溫度最高?最高溫度是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設某物體一天中的溫度![]() 是時間
是時間![]() 的函數,已知
的函數,已知![]() ,其中溫度的單位是
,其中溫度的單位是![]() ,時間的單位是小時,規定中午12:00相應的
,時間的單位是小時,規定中午12:00相應的![]() ,中午12:00以后相應的
,中午12:00以后相應的![]() 取正數,中午12:00以前相應的
取正數,中午12:00以前相應的![]() 取負數(例如早上8:00相應的
取負數(例如早上8:00相應的![]() ,下午16:00相應的
,下午16:00相應的![]() ),若測得該物體在中午12:00的溫度為
),若測得該物體在中午12:00的溫度為![]() ,在下午13:00的溫度為
,在下午13:00的溫度為![]() ,且已知該物體的溫度在早上8:00與下午16:00有相同的變化率.
,且已知該物體的溫度在早上8:00與下午16:00有相同的變化率.
(1)求該物體的溫度![]() 關于時間
關于時間![]() 的函數關系式;
的函數關系式;
(2)該物體在上午10:00至下午14:00這段時間中(包括端點)何時溫度最高?最高溫度是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某企業生產的某種產品中抽取100件,測量這些產品的質量指標值,由測量結果得到如圖所示的頻率分布直方圖,質量指標值落在區間![]() 內的頻率之比為
內的頻率之比為![]() .
.
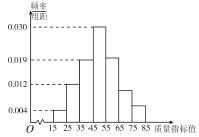
(1)求這些產品質量指標值落在區間![]() 內的頻率;
內的頻率;
(2)若將頻率視為概率,從該企業生產的這種產品中隨機抽取3件,記這3件產品中質量指標值位于區間![]() 內的產品件數為
內的產品件數為![]() ,求
,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了降低能源消耗,某冷庫內部要建造可供使用20年的隔熱層,每厘米厚的隔熱層建造成本為4萬元,又知該冷庫每年的能源消耗費用![]() (單位:萬元)與隔熱層厚度
(單位:萬元)與隔熱層厚度![]() (單位:
(單位: ![]() )滿足關系
)滿足關系![]() ,若不建隔熱層,每年能源消耗為8萬元.設
,若不建隔熱層,每年能源消耗為8萬元.設![]() 為隔熱層建造費用與20年的能源消耗費用之和.
為隔熱層建造費用與20年的能源消耗費用之和.
(1)求![]() 的值及
的值及![]() 的表達式;
的表達式;
(2)隔熱層修建多厚時,總費用![]() 達到最小?并求最小值.
達到最小?并求最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校后勤處為跟蹤調查該校餐廳的當月的服務質量,兌現獎懲,從就餐的學生中隨機抽出100位學生對餐廳服務質量打分(5分制),得到如下柱狀圖:

(1)從樣本中任意選取2名學生,求恰好有一名學生的打分不低于4分的概率;
(2)若以這100人打分的頻率作為概率,在該校隨機選取2名學生進行打分(學生打分之間相互獨立)記![]() 表示兩人打分之和,求
表示兩人打分之和,求![]() 的分布列和
的分布列和![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列程序運行后,a,b,c的值各等于什么?

(1)_____________________________________________________________.
(2)_____________________________________________________________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com