分析:(Ⅰ)由
P1(,),知
a1=,b1=,
b2==,
a2=a1b2=×=,由此能求出過點P
1,P
2直線L的方程.
(Ⅱ)由P
2坐標為(
,)得
a3=,b3=,所以點P
3∈L,猜想點P
n(n≥3,n∈N)在直線L上,再用數學歸納法證明.
(Ⅲ)由
an+1=anbn+1,bn+1=,a
k+b
k=1,知a
n≠0,a
n≠±1,所以
=+1,
{}是等差數列,由此入手能夠導出
Sn的值.
解答:解:(Ⅰ)∵
P1(,),
∴
a1=,b1=,
∴
b2==,
a2=a1b2=×=,
∴P
2坐標為(
,),(2分)
∴過點P
1,P
2直線L的方程為x+y=1,(4分)
(Ⅱ)由P
2坐標為(
,)得
a3=,b3=,
∴點P
3∈L,
猜想點P
n(n≥3,n∈N)在直線L上,以下用數學歸納法證明:
當n=3時,點P
3∈L,(5分)
假設當n=k(k≥2)時,命題成立,即點P
k∈L,
∴a
k+b
k=1,(6分)
則當n=k+1時,a
k+1+b
k+1=a
kb
k+1+b
k+1=
(1+ak)•==1,(7分)
∴點P
n∈L(n≥3),(8分)
(Ⅲ)由
an+1=anbn+1,bn+1=,a
k+b
k=1,
∴a
n≠0,a
n≠±1,
∴
an+1=an=an=,
∴
=+1,
∴
{}是等差數列,
∴
=+n-1=n+3,(9分)
∴
an=,bn=,
∵c
n+1=b
nc
n,
∴
cn=××…××c1,
=
××××1=,(10分)
∴
cnan+1==(-)(11分)
∴S
n=c
1a
2+c
2a
3+…+c
na
n+1=
[(-)+(-)+(-)+…+(-)+(-)]+(
-)]
=
[(+--)],
∴
Sn=
[(--)]=
[(--)]=
.(12分)
點評:本題考查數列和解析幾何的綜合運用,解題時要認真審題,注意挖掘題設中的隱含條件.



 全優考典單元檢測卷及歸類總復習系列答案
全優考典單元檢測卷及歸類總復習系列答案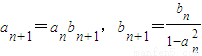 ,且
,且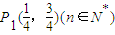 .
.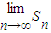 的值.
的值.