
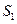 、
、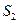 、
、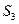 ,試判斷S
,試判斷S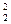 =4
=4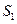
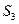 是否成立,并證明你的結論.
是否成立,并證明你的結論. ,0),準線l的方程為x=-
,0),準線l的方程為x=- .
. ,則有M1(-
,則有M1(- ,y1),N1(-
,y1),N1(- ,y2),
,y2),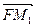 =(-p,y1),
=(-p,y1), 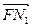 =(-p,y2).
=(-p,y2).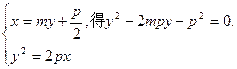
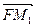 ·
·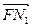 =p2+y1y2=p2-p2=0,故FM1⊥FN1.
=p2+y1y2=p2-p2=0,故FM1⊥FN1.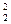 =4S1S3成立,證明如下:
=4S1S3成立,證明如下: , |NN1|=|NF|=x2+
, |NN1|=|NF|=x2+ . 于是
. 于是 ·|MM1|·|F1M1|=
·|MM1|·|F1M1|= (x1+
(x1+ )|y1|,
)|y1|, ·|M1N1|·|FF1|=
·|M1N1|·|FF1|= p|y1-y2|,
p|y1-y2|, ·|NN1|·|F1N1|=
·|NN1|·|F1N1|= (x2+
(x2+ )|y2|,
)|y2|,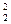 =4S1S3
=4S1S3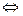 (
( p|y1-y2|)2
p|y1-y2|)2 (x1+
(x1+ )|y1|·
)|y1|· (x2+
(x2+ )·|y2|
)·|y2|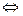
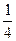 p2[(y1+y2)2-4y1y2]=[x1x2+
p2[(y1+y2)2-4y1y2]=[x1x2+ (x1+x2)+
(x1+x2)+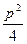 ]·|y1y2|.
]·|y1y2|. 與
與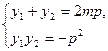 代入上式化簡可得
代入上式化簡可得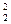 =4S1S3成立.
=4S1S3成立.

 口算能手系列答案
口算能手系列答案科目:高中數學 來源:不詳 題型:解答題
 , 過拋物線C上點M且與M處的切線垂直的直線稱為拋物線C在點M的法線。
, 過拋物線C上點M且與M處的切線垂直的直線稱為拋物線C在點M的法線。 ,求點M的坐標
,求點M的坐標 ;
;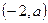 為C對稱軸上的一點,在C上是否存在點,使得C在該點的法線通過點P。若有,求出這些點,以及C在這些點的法線方程;若沒有,請說明理由。
為C對稱軸上的一點,在C上是否存在點,使得C在該點的法線通過點P。若有,求出這些點,以及C在這些點的法線方程;若沒有,請說明理由。查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com