
���}Ŀ����֪�A![]() �ĈA����ֱ��
�ĈA����ֱ��![]() �ϣ����^(gu��)�c(di��n)
�ϣ����^(gu��)�c(di��n)![]() ���cֱ��
���cֱ��![]() ���У�
����
��![]() ����A
����A![]() �ķ�����
�ķ�����
��![]() ���O(sh��)ֱ��
���O(sh��)ֱ��![]() �c�A
�c�A![]() �ཻ��
�ཻ��![]() ��
��![]() ���c(di��n)����(sh��)��(sh��)
���c(di��n)����(sh��)��(sh��)![]() ��ȡֵ������
��ȡֵ������
��![]() ������
������![]() ���ėl���£��Ƿ���ڌ�(sh��)��(sh��)
���ėl���£��Ƿ���ڌ�(sh��)��(sh��)![]() ��ʹ����
��ʹ����![]() �Ĵ�ֱƽ�־�
�Ĵ�ֱƽ�־�![]() �^(gu��)�c(di��n)
�^(gu��)�c(di��n)![]() �������ڣ������(sh��)��(sh��)
�������ڣ������(sh��)��(sh��)![]() ��ֵ���������ڣ�Ո(q��ng)�f(shu��)��������
��ֵ���������ڣ�Ո(q��ng)�f(shu��)��������
���𰸡���1��![]() ����2��
����2��![]() ����3��Ҋ(ji��n)����.
����3��Ҋ(ji��n)����.
����������ԇ�}��Ҫ�ǿ����˾��c�A��λ���P(gu��n)ϵ�ľC���\(y��n)�á�
��1����?y��n)�AC�ĈA����ֱ��y=x+1�ϣ����^(gu��)�c(di��n)![]() ��1��3�����cֱ��x+2y-7=0����. ���ÈA�ĵ�ֱ���ľ��x���ڈA�İ돽�õ��Y(ji��)Փ��
��1��3�����cֱ��x+2y-7=0����. ���ÈA�ĵ�ֱ���ľ��x���ڈA�İ돽�õ��Y(ji��)Փ��
��2����?y��n)�ֱ���c�A�ཻ���t�A�ĵ�ֱ���ľ��xС�ڈA�İ돽�õ�����(sh��)a�ķ�����
��3���O(sh��)���ϗl���Č�(sh��)��(sh��)![]() ���ڣ�����
���ڣ�����![]() ���tֱ��
���tֱ��![]() ��б�ʞ�
��б�ʞ�![]() ��
��![]() �ķ��̞�
�ķ��̞�![]() ����
����![]() ������
������![]() ��ֱƽ���ң��ʈA��
��ֱƽ���ң��ʈA��![]()
![]() �ϣ��Ķ��õ���
�ϣ��Ķ��õ���
�⣺��1����?y��n)�AC�ĈA����ֱ��y=x+1�ϣ����O(sh��)�A������(bi��o)��![]() �����}����з�
�����}����з�
��![]() �����
�����![]() �����ԈA������(bi��o)�飨
�����ԈA������(bi��o)�飨![]() �����돽
�����돽
��![]() �����ԈA�ķ��̞�
�����ԈA�ķ��̞�![]() ��-----------------5��
��-----------------5��
(2)(li��n)������![]() ����
����![]() ��
��![]() ������ֱ���c�A����
������ֱ���c�A����![]() ���c(di��n)������
���c(di��n)������![]() �����
�����![]() ������
������![]() ��ȡֵ�����ǣ�
��ȡֵ�����ǣ�![]() ��------8�֣�3���O(sh��)���ϗl���Č�(sh��)��(sh��)
��------8�֣�3���O(sh��)���ϗl���Č�(sh��)��(sh��)![]() ���ڣ�����
���ڣ�����![]() ���tֱ��
���tֱ��![]() ��б�ʞ�
��б�ʞ�![]() ��
��![]() �ķ��̞�
�ķ��̞�![]() ����
����![]() ������
������![]() ��ֱƽ���ң��ʈA��
��ֱƽ���ң��ʈA��![]()
![]() �ϣ�
�ϣ�
����![]() �����
�����![]() ������
������![]() ���ʲ����ڌ�(sh��)��(sh��)
���ʲ����ڌ�(sh��)��(sh��)![]() ��ʹ���^(gu��)�c(di��n)
��ʹ���^(gu��)�c(di��n)![]() ��ֱ����ֱƽ����.--------------13��
��ֱ����ֱƽ����.--------------13��



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�c(di��n)![]() �ǒ��タ
�ǒ��タ![]() �Ľ��c(di��n), ���c(di��n)
�Ľ��c(di��n), ���c(di��n)![]() ��
��![]() ��,��
��,��![]() ��
��
��1����![]() ��ֵ��
��ֵ��
��2����ֱ��![]() ��(j��ng)�^(gu��)�c(di��n)
��(j��ng)�^(gu��)�c(di��n)![]() ���c
���c![]() ����
����![]() ������
������![]() �����c(di��n), �C��: ֱ��
�����c(di��n), �C��: ֱ��![]() �cֱ��
�cֱ��![]() ��б��֮�e�鳣��(sh��)��
��б��֮�e�鳣��(sh��)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����˸��õ�Ҏ(gu��)���M(j��n)؛�Ĕ�(sh��)�������C�߲˵����r�̶ȣ�ij�߲��̵��ijһ����N�۔�(sh��)��(j��)�У��S�C(j��)��ȡ��8�M��(sh��)��(j��)�����о���(du��)�����D��ʾ��![]() ���������I�M(j��n)�߲˵��|(zh��)����
���������I�M(j��n)�߲˵��|(zh��)���� ![]() ���죩���N���씵(sh��)����
���죩���N���씵(sh��)����
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
������(j��)�ϱ픵(sh��)��(j��)�����оW(w��ng)�����L��ɢ�c(di��n)�D��

������(j��)�ϱ��ṩ�Ĕ�(sh��)��(j��)������С���˷����![]() �P(gu��n)��
�P(gu��n)��![]() �ľ��Իؚw����
�ľ��Իؚw����![]() ��
��
������(j��)�����е�Ӌ(j��)��Y(ji��)������ԓ�߲��̵��(zh��n)��һ�����I�M(j��n)25�����t�A(y��)Ӌ(j��)��Ҫ�N�۶�����.
������ʽ��  ��
�� ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��2016�괺��(ji��),�����t�����ɞ����(hu��)���h��Ԓ�}֮һ.ij�C(j��)��(g��u)��(du��)����(ji��)���g�Ñ������֙C(j��)�����t��������r�M(j��n)���{(di��o)��,���һ���(n��i)���t���Ŀ��Δ�(sh��)���^(gu��)10�Ξ顰�P(gu��n)ע�c(di��n)�ߡ�,��t�顰�P(gu��n)ע�c(di��n)�͡�,�{(di��o)����r���±���ʾ:

(1)��ϱ���x,y��ֵ���Д��Ƿ���95%���ϵİ����J(r��n)���Ԅe�c�P(gu��n)ע�c(di��n)�ߵ����P(gu��n)?
(2)�F(xi��n)Ҫ�����������Ñ����S�C(j��)�x��3������һ�(xi��ng)���(d��ng),��X��ʾ�x�е�ͬ�W(xu��)�Г��t�����Δ�(sh��)���^(gu��)10�ε��˔�(sh��),���S�C(j��)׃��X�ķֲ��м���(sh��)�W(xu��)����E(X).
������R��ֵ��������:

��(d��)���ԙz�(y��n)�y(t��ng)Ӌ(j��)�� ,����n=a+b+c+d.
,����n=a+b+c+d.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
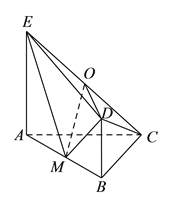
���}Ŀ����D��ƽ��![]() ƽ��
ƽ��![]() ��
��![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�![]() ����߅��
����߅��![]() ��ֱ�����Σ�
��ֱ�����Σ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �քe��
�քe��![]() ��
��![]() �����c(di��n)��
�����c(di��n)��
��I�����C��![]() ƽ��
ƽ��![]() ��
��
��II����ֱ��![]() ��ƽ��
��ƽ��![]() ���ɽǵ�����ֵ��
���ɽǵ�����ֵ��
��III���ܷ���![]() ����һ�c(di��n)
����һ�c(di��n)![]() ��ʹ��
��ʹ��![]() ƽ��
ƽ��![]() ?���ܣ�Ո(q��ng)ָ���c(di��n)
?���ܣ�Ո(q��ng)ָ���c(di��n)![]() ��λ�ã��������C���������ܣ�Ո(q��ng)�f(shu��)��������
��λ�ã��������C���������ܣ�Ո(q��ng)�f(shu��)��������
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���Ѳ���ʽ�M ![]() �Ľ⼯��ʾ�ڔ�(sh��)�S�ϣ����_���ǣ�������
�Ľ⼯��ʾ�ڔ�(sh��)�S�ϣ����_���ǣ�������
A.![]()
B.![]()
C.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D,��֪��߅��![]() ��ֱ�����Σ�
��ֱ�����Σ� ![]() ,��
,��![]() ����
����![]() ���߅�ĵ���ֱ�������Σ���
���߅�ĵ���ֱ�������Σ���![]() .
.

��1���C���� ![]() ƽ��
ƽ��![]() ��
��
��2����ֱ��![]() �cƽ��
�cƽ��![]() ���ɵĽǵĴ�С.
���ɵĽǵĴ�С.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D�� ![]() ��߅�L(zh��ng)��
��߅�L(zh��ng)��![]() �����Σ�
������ ![]() ��
�� ![]() ƽ��
ƽ��![]() ��
�� ![]() ƽ��
ƽ��![]() ��
�� ![]() .
.
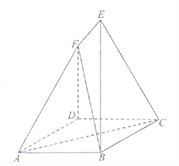
�������C�� ![]() ��
��
������ֱ��![]() �cƽ��
�cƽ��![]() ���ɽǵ�����ֵ.
���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��ֱ������![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ���c(di��n)
���c(di��n)![]() �ھ���
�ھ���![]() ��.
��.

�����C��![]() ��
��
������![]() ��
��![]() ���c(di��n)���C��
���c(di��n)���C��![]() ƽ��
ƽ��![]() ��
��
����(d��ng)![]() �r(sh��)��������
�r(sh��)��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com