
【題目】某綜藝節目為增強娛樂性,要求現場嘉賓與其場外好友連線互動.凡是拒絕表演節目的好友均無連線好友的機會;凡是選擇表演節目的好友均需連線未參加過此活動的3個好友參與此活動,以此下去.
(Ⅰ)假設每個人選擇表演與否是等可能的,且互不影響,則某人選擇表演后,其連線的3個好友中不少于2個好友選擇表演節目的概率是多少?
(Ⅱ)為調查“選擇表演者”與其性別是否有關,采取隨機抽樣得到如表:
選擇表演 | 拒絕表演 | 合計 | |
男 | 50 | 10 | 60 |
女 | 10 | 10 | 20 |
合計 | 60 | 20 | 80 |
①根據表中數據,是否有99%的把握認為“表演節目”與好友的性別有關?
②將此樣本的頻率視為總體的概率,隨機調查3名男性好友,設X為3個人中選擇表演的人數,求X的分布列和期望.
附:K2= ![]() ;
;
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【答案】解:(Ⅰ)這3位好友選擇表演分別記為A,B,C,則 ![]() ,
, ![]() ,
, ![]() 分別表示這3位好友拒絕表演.這3位好友參與該活動的可能結果為{A,B,C},{
分別表示這3位好友拒絕表演.這3位好友參與該活動的可能結果為{A,B,C},{ ![]() ,B,C},{A,
,B,C},{A, ![]() ,C},{A,B,
,C},{A,B, ![]() },{
},{ ![]() ,
, ![]() ,C},{A,
,C},{A, ![]() ,
, ![]() },{
},{ ![]() ,B,
,B, ![]() },{
},{ ![]() ,
, ![]() ,
, ![]() }共有8種.其中3位好友不少于3位好友選擇表演的可能結果有4種.根據古典概型公式,所求概率為P=
}共有8種.其中3位好友不少于3位好友選擇表演的可能結果有4種.根據古典概型公式,所求概率為P= ![]() =
= ![]() ;
;
(Ⅱ)①根據2×2列聯表,得到K2= ![]() ≈8.9>6.635,所以有99%的把握認為“表演節目”與好友的性別有關.
≈8.9>6.635,所以有99%的把握認為“表演節目”與好友的性別有關.
②由題意,每名男性選擇表演的概率為 ![]() ,則X~B(3,
,則X~B(3, ![]() ),
),
所以隨機變量X的概率分布列為:
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
故隨機變量X的期望為EX=3× ![]() =
= ![]()
【解析】(Ⅰ)利用列舉法,確定基本事件的個數,即可求出概率;(Ⅱ)①根據2×2列聯表,得到K2= ![]() ≈8.9>6.635,即可得出結論;②由題意,每名男性選擇表演的概率為
≈8.9>6.635,即可得出結論;②由題意,每名男性選擇表演的概率為 ![]() ,則X~B(3,
,則X~B(3, ![]() ),可得X的分布列和期望.
),可得X的分布列和期望.


科目:高中數學 來源: 題型:
【題目】隨機擲兩枚質地均勻的骰子,它們向上的點數之和不超過5的概率記為p1,點數之和大于5的概率記為p2,點數之和為偶數的概率記為p3,則( )
A. p1<p2<p3 B. p2<p1<p3
C. p1<p3<p2 D. p3<p1<p2
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,多面體EF﹣ABCD中,ABCD是正方形,AC、BD相交于O,EF∥AC,點E在AC上的射影恰好是線段AO的中點.
(Ⅰ)求證:BD⊥平面ACF;
(Ⅱ)若直線AE與平面ABCD所成的角為60°,求平面DEF與平面ABCD所成角的正弦值.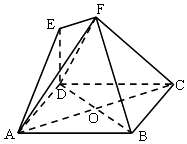
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖下圖①,等邊三角形ABC的邊長為2a,CD是AB邊上的高,E,F分別是AC和BC邊上的點,且滿足![]() =k,現將△ABC沿CD翻折成直二面角ADCB,如圖下圖②.
=k,現將△ABC沿CD翻折成直二面角ADCB,如圖下圖②.
(1)試判斷翻折后直線AB與平面DEF的位置關系,并說明理由;
(2)求二面角BACD的正切值.
① ②
②
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某班同學利用寒假進行社會實踐活動,對![]() 歲的人群隨機抽取
歲的人群隨機抽取![]() 人進行了一次生活習慣是
人進行了一次生活習慣是
否符合低碳觀念的調查,若生活習慣符合低碳觀念的稱為“低碳族”,否則稱為“非低碳族”,得
到如下統計表和各年齡段人數頻率分布直方圖:
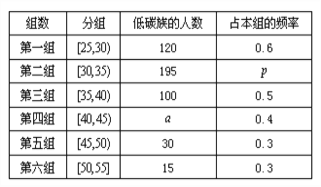
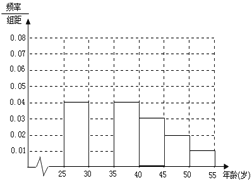
(I)補全頻率分布直方圖并求![]() 、
、![]() 、
、![]() 的值;
的值;
(II)從年齡段在![]() 的“低碳族”中采用分層抽樣法抽取
的“低碳族”中采用分層抽樣法抽取![]() 人參加戶外低碳體驗活動,其中選取
人參加戶外低碳體驗活動,其中選取![]() 人作為領隊,求選取的
人作為領隊,求選取的![]() 名領隊中恰有1人年齡在
名領隊中恰有1人年齡在![]() 歲的概率.
歲的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】農科院的專家為了了解新培育的甲、乙兩種麥苗的長勢情況,從甲、乙兩種麥苗的試驗田中各抽取6株麥苗測量麥苗的株高,數據如下:(單位:cm)
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21.
(1)在給出的方框內繪出所抽取的甲、乙兩種麥苗株高的莖葉圖;
(2)分別計算所抽取的甲、乙兩種麥苗株高的平均數與方差,并由此判斷甲、乙兩種麥苗的長勢情況.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地區交管部門為了對該地區駕駛員的某項考試成績進行分析,隨機抽取了15分到45分之間的1000名學員的成績,并根據這1000名駕駛員的成績畫出樣本的頻率分布直方圖(如圖),則成績在[30,35)內的駕駛員人數共有( ) 
A.60
B.180
C.300
D.360
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() :
: ![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
, ![]() 兩點,記拋物線在
兩點,記拋物線在![]() ,
, ![]() 兩點處的切線
兩點處的切線![]() ,
, ![]() 的交點為
的交點為![]() .
.
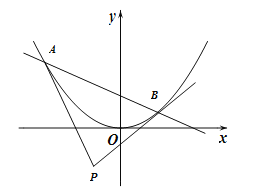
(I)求證: ![]() ;
;
(II)求點![]() 的坐標(用
的坐標(用![]() ,
, ![]() 表示);
表示);
(Ⅲ)若![]() ,求△
,求△![]() 的面積的最小值.
的面積的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com