
(本小題共14分)函數 ,
,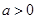 ,
, .
.
(1)①試用含有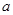 的式子表示
的式子表示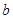 ;②求
;②求 的單調區間;
的單調區間;
(2)對于函數圖像上的不同兩點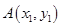 ,
, ,如果在函數圖像上存在點
,如果在函數圖像上存在點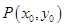 (其中
(其中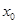 在
在 與
與 之間),使得點
之間),使得點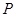 處的切線
處的切線 ∥
∥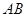 ,則稱
,則稱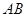 存在“伴隨切線”,當
存在“伴隨切線”,當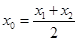 時,又稱
時,又稱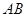 存在“中值伴隨切線”。試問:在函數
存在“中值伴隨切線”。試問:在函數 的圖像上是否存在兩點
的圖像上是否存在兩點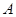 、
、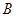 ,使得
,使得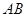 存在“中值伴隨切線”?若存在,求出
存在“中值伴隨切線”?若存在,求出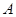 、
、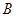 的坐標;若不存在,說明理由。
的坐標;若不存在,說明理由。
科目:高中數學 來源: 題型:
(本小題共14分)
已知函數![]() 與
與![]() 的圖象相交于
的圖象相交于![]() ,
,![]() ,
,![]() ,
,![]() 分別是
分別是![]() 的圖象在
的圖象在![]() 兩點的切線,
兩點的切線,![]() 分別是
分別是![]() ,
,![]() 與
與![]() 軸的交點.
軸的交點.
(I)求![]() 的取值范圍;
的取值范圍;
(II)設![]() 為點
為點![]() 的橫坐標,當
的橫坐標,當![]() 時,寫出
時,寫出![]() 以
以![]() 為自變量的函數式,并求其定義域和值域;
為自變量的函數式,并求其定義域和值域;
(III)試比較![]() 與
與![]() 的大小,并說明理由(
的大小,并說明理由(![]() 是坐標原點).
是坐標原點).
查看答案和解析>>
科目:高中數學 來源: 題型:
(07年北京卷)(本小題共14分)
如圖,矩形![]() 的兩條對角線相交于點
的兩條對角線相交于點![]() ,
,![]() 邊所在直線的方程為
邊所在直線的方程為![]() 點
點![]() 在
在![]() 邊所在直線上.
邊所在直線上.
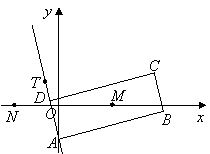
(I)求![]() 邊所在直線的方程;
邊所在直線的方程;
(II)求矩形![]() 外接圓的方程;
外接圓的方程;
(III)若動圓![]() 過點
過點![]() ,且與矩形
,且與矩形![]() 的外接圓外切,求動圓
的外接圓外切,求動圓![]() 的圓心的軌跡方程.
的圓心的軌跡方程.
查看答案和解析>>
科目:高中數學 來源:2011-2012學年北京市高三壓軸文科數學試卷(解析版) 題型:解答題
(本小題共14分)
已知函數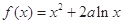 .
.
(Ⅰ)若函數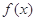 的圖象在
的圖象在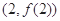 處的切線斜率為
處的切線斜率為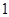 ,求實數
,求實數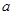 的值;
的值;
(Ⅱ)求函數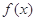 的單調區間;
的單調區間;
(Ⅲ)若函數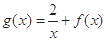 在
在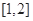 上是減函數,求實數
上是減函數,求實數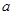 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010年北京市宣武區高三第二次模擬考試數學(理) 題型:解答題
(本小題共14分)
已知函數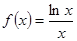 .
.
(I)判斷函數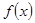 的單調性;
的單調性;
(Ⅱ)若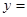
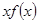 +
+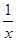 的圖像總在直線
的圖像總在直線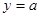 的上方,求實數
的上方,求實數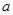 的取值范圍;
的取值范圍;
(Ⅲ)若函數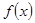 與
與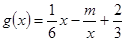 的圖像有公共點,且在公共點處的切線相同,求實數
的圖像有公共點,且在公共點處的切線相同,求實數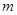 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com